Refine listing
Actions for selected content:
616 results in 20Cxx
Elements of minimal breadth in finite p-groups and lie algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 2 / October 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 209-214
- Print publication:
- October 2006
-
- Article
-
- You have access
- Export citation
Class preserving automorphisms of Blackburn groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 3 / June 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 351-358
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
Group algebras with an Engel group of units
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 2 / April 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 173-178
- Print publication:
- April 2006
-
- Article
-
- You have access
- Export citation
Some new permutability properties of hypercentrally embedded subgroups of finite groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 2 / October 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 243-255
- Print publication:
- October 2005
-
- Article
-
- You have access
- Export citation
The k(GV)-problem revisited
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 2 / October 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 257-276
- Print publication:
- October 2005
-
- Article
-
- You have access
- Export citation
Finite p–nilpotent groups with some subgroups c–supplemented
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 3 / June 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 429-439
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation
On c-normality of finite groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 3 / June 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 297-304
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation
On supersoluble groups of Wielandt length two
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 3 / June 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 393-406
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation
Finite group with Hall coverings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 1 / February 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-16
- Print publication:
- February 2005
-
- Article
-
- You have access
- Export citation
Modular Lie representations of finite groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 3 / December 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 401-424
- Print publication:
- December 2004
-
- Article
-
- You have access
- Export citation
Certain relations between p-regular class sizes and the p-structure of p-solvable groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 3 / December 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 387-400
- Print publication:
- December 2004
-
- Article
-
- You have access
- Export citation
On the orders of conjugacy classes in group algebras of p-groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 2 / October 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 185-190
- Print publication:
- October 2004
-
- Article
-
- You have access
- Export citation
Fitting classes and lattice formations II
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 175-188
- Print publication:
- April 2004
-
- Article
-
- You have access
- Export citation
On Local Embedding Properties of Injectors of Finite Soluble Groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 1 / February 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 23-38
- Print publication:
- February 2004
-
- Article
-
- You have access
- Export citation
Fitting classes and lattice formations I
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 1 / February 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 93-108
- Print publication:
- February 2004
-
- Article
-
- You have access
- Export citation
On finite J-groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 2 / October 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 181-192
- Print publication:
- October 2003
-
- Article
-
- You have access
- Export citation
A new approach to the k(GV)-problem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 2 / October 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 193-220
- Print publication:
- October 2003
-
- Article
-
- You have access
- Export citation
Betti numbers of fixed point sets and multiplicities of indecomposable summands
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 2 / April 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 165-172
- Print publication:
- April 2003
-
- Article
-
- You have access
- Export citation
Strong duality for metacyclic groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 3 / December 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 377-392
- Print publication:
- December 2002
-
- Article
-
- You have access
- Export citation
The module structure of Solomon's descent algebra
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 3 / June 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 317-334
- Print publication:
- June 2002
-
- Article
-
- You have access
- Export citation
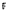 a field of
a field of 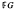 has a conjugacy class of
has a conjugacy class of 