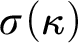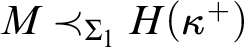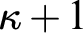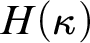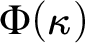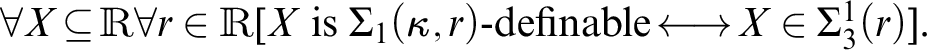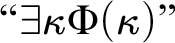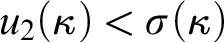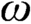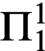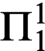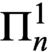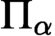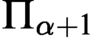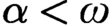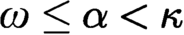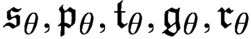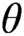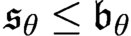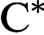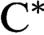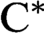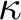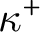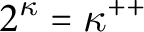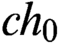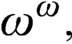Refine listing
Actions for selected content:
374 results in 03EXX
STABLY MEASURABLE CARDINALS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 15 June 2020, pp. 448-470
- Print publication:
- June 2021
-
- Article
- Export citation
COMPLETELY SEPARABLE MAD FAMILIES AND THE MODAL LOGIC OF βω
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 15 June 2020, pp. 498-507
- Print publication:
- June 2022
-
- Article
- Export citation
N-BERKELEY CARDINALS AND WEAK EXTENDER MODELS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 21 July 2020, pp. 809-816
- Print publication:
- June 2020
-
- Article
- Export citation
THE KETONEN ORDER
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 18 June 2020, pp. 585-604
- Print publication:
- June 2020
-
- Article
- Export citation
HOW STRONG ARE SINGLE FIXED POINTS OF NORMAL FUNCTIONS?
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 20 July 2020, pp. 709-732
- Print publication:
- June 2020
-
- Article
- Export citation
THE COMPLEXITY OF HOMEOMORPHISM RELATIONS ON SOME CLASSES OF COMPACTA
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 18 June 2020, pp. 733-748
- Print publication:
- June 2020
-
- Article
- Export citation
A REFINEMENT OF THE RAMSEY HIERARCHY VIA INDESCRIBABILITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 22 June 2020, pp. 773-808
- Print publication:
- June 2020
-
- Article
- Export citation
ON CONFIGURATIONS CONCERNING CARDINAL CHARACTERISTICS AT REGULAR CARDINALS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 10 July 2020, pp. 691-708
- Print publication:
- June 2020
-
- Article
- Export citation
A RECONSTRUCTION OF STEEL’S MULTIVERSE PROJECT
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 26 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 11 June 2020, pp. 118-169
- Print publication:
- June 2020
-
- Article
-
- You have access
- Open access
- Export citation
VOICULESCU’S THEOREM FOR NONSEPARABLE
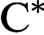 $\text{C}^{\ast} $-ALGEBRAS
$\text{C}^{\ast} $-ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 20 July 2020, pp. 624-631
- Print publication:
- June 2020
-
- Article
-
- You have access
- Open access
- Export citation
Sigma-Prikry forcing I: The Axioms
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 26 May 2020, pp. 1205-1238
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- Export citation
Maximally highly proximal flows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 18 May 2020, pp. 2220-2240
- Print publication:
- July 2021
-
- Article
- Export citation
AN APPLICATION OF RECURSION THEORY TO ANALYSIS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 26 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 11 June 2020, pp. 15-25
- Print publication:
- March 2020
-
- Article
- Export citation
NONMEASURABLE SETS AND UNIONS WITH RESPECT TO TREE IDEALS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 26 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 19 June 2020, pp. 1-14
- Print publication:
- March 2020
-
- Article
- Export citation
MEASURABLE REALIZATIONS OF ABSTRACT SYSTEMS OF CONGRUENCES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 24 February 2020, e10
-
- Article
-
- You have access
- Open access
- Export citation
On Baire measurable colorings of group actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 10 January 2020, pp. 818-845
- Print publication:
- March 2021
-
- Article
- Export citation
THE QUANDARY OF QUANDLES: A BOREL COMPLETE KNOT INVARIANT
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 30 October 2019, pp. 262-277
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
CONTINUITY OF UNIVERSALLY MEASURABLE HOMOMORPHISMS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 7 / 2019
- Published online by Cambridge University Press:
- 13 August 2019, e5
-
- Article
-
- You have access
- Open access
- Export citation
On the existence of cocycle-invariant Borel probability measures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 12 April 2019, pp. 3150-3168
- Print publication:
- November 2020
-
- Article
- Export citation
Hyperfiniteness of boundary actions of cubulated hyperbolic groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 25 March 2019, pp. 2453-2466
- Print publication:
- September 2020
-
- Article
- Export citation