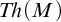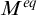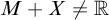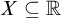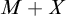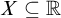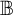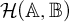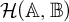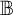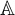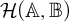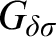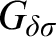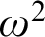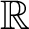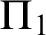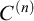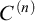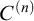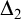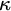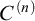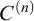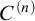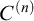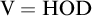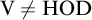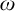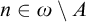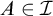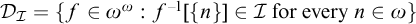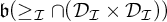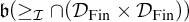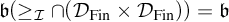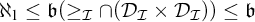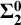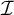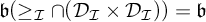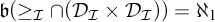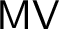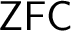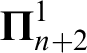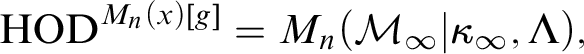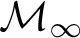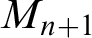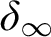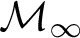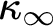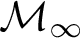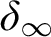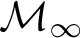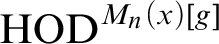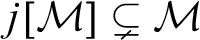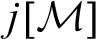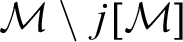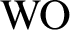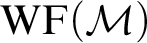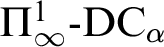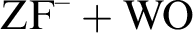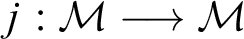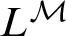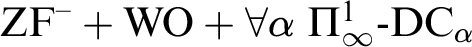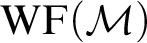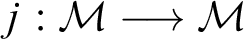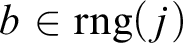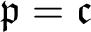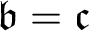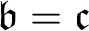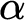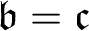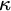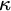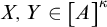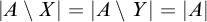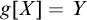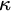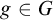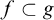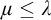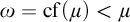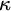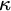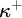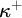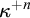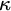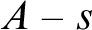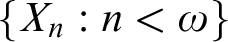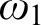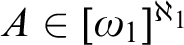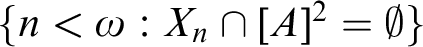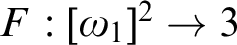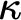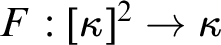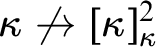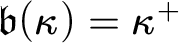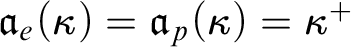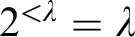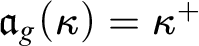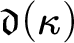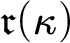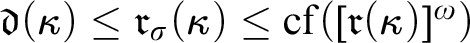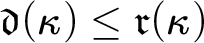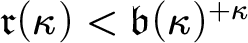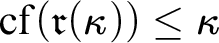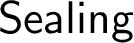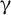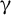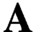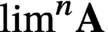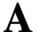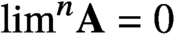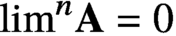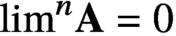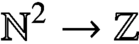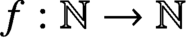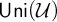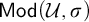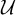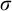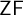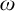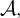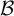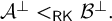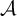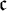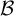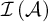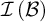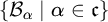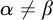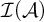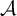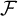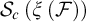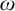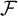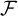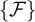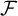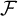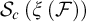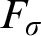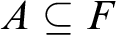Refine listing
Actions for selected content:
374 results in 03EXX
MOST(?) THEORIES HAVE BOREL COMPLETE REDUCTS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 27 September 2021, pp. 418-426
- Print publication:
- March 2023
-
- Article
- Export citation
MEAGER-ADDITIVE SETS IN TOPOLOGICAL GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 27 September 2021, pp. 1046-1064
- Print publication:
- September 2022
-
- Article
- Export citation
ON SEQUENCES OF HOMOMORPHISMS INTO MEASURE ALGEBRAS AND THE EFIMOV PROBLEM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 13 September 2021, pp. 191-218
- Print publication:
- March 2023
-
- Article
- Export citation
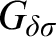 $G_{\delta \sigma }$ GAMES AND INDUCTION ON REALS
$G_{\delta \sigma }$ GAMES AND INDUCTION ON REALS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 13 September 2021, pp. 1676-1690
- Print publication:
- December 2021
-
- Article
- Export citation
MORE ON THE PRESERVATION OF LARGE CARDINALS UNDER CLASS FORCING
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 13 September 2021, pp. 290-323
- Print publication:
- March 2023
-
- Article
- Export citation
YET ANOTHER IDEAL VERSION OF THE BOUNDING NUMBER
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 13 September 2021, pp. 1065-1092
- Print publication:
- September 2022
-
- Article
- Export citation
STEEL’S PROGRAMME: EVIDENTIAL FRAMEWORK, THE CORE AND ULTIMATE-L
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 31 August 2021, pp. 788-812
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
 $\operatorname {HOD}$ IN INNER MODELS WITH WOODIN CARDINALS
$\operatorname {HOD}$ IN INNER MODELS WITH WOODIN CARDINALS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 13 August 2021, pp. 871-896
- Print publication:
- September 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INITIAL SELF-EMBEDDINGS OF MODELS OF SET THEORY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 13 August 2021, pp. 1584-1611
- Print publication:
- December 2021
-
- Article
- Export citation
THE RUDIN–KEISLER ORDERING OF P-POINTS UNDER 𝔟 = 𝔠
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 13 August 2021, pp. 1691-1705
- Print publication:
- December 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON
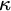 $\kappa $-HOMOGENEOUS, BUT NOT
$\kappa $-HOMOGENEOUS, BUT NOT 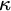 $\kappa $-TRANSITIVE PERMUTATION GROUPS
$\kappa $-TRANSITIVE PERMUTATION GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 13 August 2021, pp. 363-380
- Print publication:
- March 2023
-
- Article
- Export citation
NOTES ON SOME ERDŐS–HAJNAL PROBLEMS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 12 August 2021, pp. 1116-1123
- Print publication:
- September 2021
-
- Article
- Export citation
MORE ZFC INEQUALITIES BETWEEN CARDINAL INVARIANTS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 02 August 2021, pp. 897-912
- Print publication:
- September 2021
-
- Article
- Export citation
A non-Borel special alpha-limit set in the square
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 22 July 2021, pp. 2550-2560
- Print publication:
- August 2022
-
- Article
- Export citation
SEALING OF THE UNIVERSALLY BAIRE SETS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 02 July 2021, pp. 254-266
- Print publication:
- September 2021
-
- Article
- Export citation
NULL SETS AND COMBINATORIAL COVERING PROPERTIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 15 June 2021, pp. 1231-1242
- Print publication:
- September 2022
-
- Article
- Export citation
Simultaneously vanishing higher derived limits
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 9 / 2021
- Published online by Cambridge University Press:
- 14 June 2021, e4
-
- Article
-
- You have access
- Open access
- Export citation
THE COPERNICAN MULTIVERSE OF SETS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 14 June 2021, pp. 1033-1069
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MORE ON FRÉCHET–URYSOHN IDEALS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 10 June 2021, pp. 829-851
- Print publication:
- June 2022
-
- Article
- Export citation
COUNTABLY PERFECTLY MEAGER SETS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 07 June 2021, pp. 1214-1227
- Print publication:
- September 2021
-
- Article
- Export citation