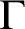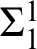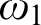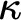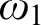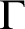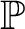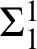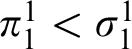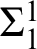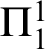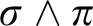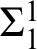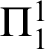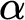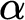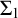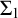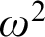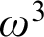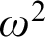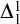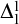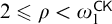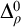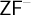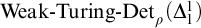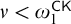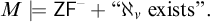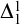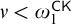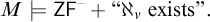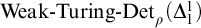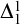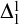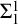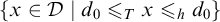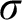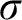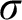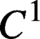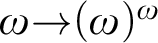Refine listing
Actions for selected content:
374 results in 03EXX
COMBINING RESURRECTION AND MAXIMALITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 02 February 2021, pp. 397-414
- Print publication:
- March 2021
-
- Article
- Export citation
AUTOMATIC CONTINUITY FOR ISOMETRY GROUPS – ERRATUM
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 02 February 2021, pp. 2253-2255
- Print publication:
- November 2022
-
- Article
- Export citation
ON THE AUTOMORPHISM GROUP OF THE UNIVERSAL HOMOGENEOUS MEET-TREE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 1508-1540
- Print publication:
- December 2021
-
- Article
- Export citation
CHARACTERIZING EXISTENCE OF A MEASURABLE CARDINAL VIA MODAL LOGIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 162-177
- Print publication:
- March 2021
-
- Article
- Export citation
ARONSZAJN TREE PRESERVATION AND BOUNDED FORCING AXIOMS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 293-315
- Print publication:
- March 2021
-
- Article
- Export citation
Minimal definable graphs of definable chromatic number at least three
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 28 January 2021, e7
-
- Article
-
- You have access
- Open access
- Export citation
IDEAL INDEPENDENT FAMILIES AND THE ULTRAFILTER NUMBER
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 08 January 2021, pp. 128-136
- Print publication:
- March 2021
-
- Article
- Export citation
THE ORDER OF REFLECTION
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 08 January 2021, pp. 1555-1583
- Print publication:
- December 2021
-
- Article
- Export citation
THE Σ1-DEFINABLE UNIVERSAL FINITE SEQUENCE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 08 January 2021, pp. 783-801
- Print publication:
- June 2022
-
- Article
- Export citation
SHORTENING CLOPEN GAMES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 08 January 2021, pp. 1541-1554
- Print publication:
- December 2021
-
- Article
- Export citation
VARIATIONS ON
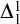 $\Delta ^{1}_{1}$ DETERMINACY AND ℵω1
$\Delta ^{1}_{1}$ DETERMINACY AND ℵω1
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 07 January 2021, pp. 721-731
- Print publication:
- June 2022
-
- Article
- Export citation
On Polish groups admitting non-essentially countable actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 29 December 2020, pp. 180-194
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- Export citation
Proof of a conjecture of Galvin
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 21 December 2020, e15
-
- Article
-
- You have access
- Open access
- Export citation
Decompositions and measures on countable Borel equivalence relations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 04 December 2020, pp. 3671-3703
- Print publication:
- December 2021
-
- Article
- Export citation
THE MODAL LOGIC OF
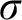 $\sigma $-CENTERED FORCING AND RELATED FORCING CLASSES
$\sigma $-CENTERED FORCING AND RELATED FORCING CLASSES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1-24
- Print publication:
- March 2021
-
- Article
- Export citation
TWO ARGUMENTS AGAINST THE GENERIC MULTIVERSE
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 14 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 02 December 2020, pp. 347-379
- Print publication:
- June 2021
-
- Article
- Export citation
RANK-TO-RANK EMBEDDINGS AND STEEL’S CONJECTURE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 13 November 2020, pp. 137-147
- Print publication:
- March 2021
-
- Article
- Export citation
A dichotomy of sets via typical differentiability
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 04 November 2020, e41
-
- Article
-
- You have access
- Open access
- Export citation
Cardinal invariants of Haar null and Haar meager sets
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 27 October 2020, pp. 1568-1594
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- Export citation
CLASSES OF BARREN EXTENSIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 05 October 2020, pp. 178-209
- Print publication:
- March 2021
-
- Article
- Export citation