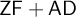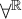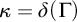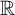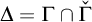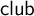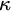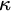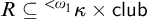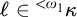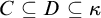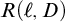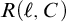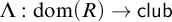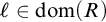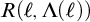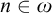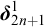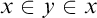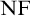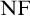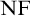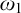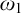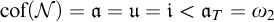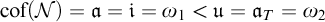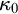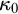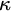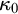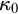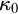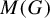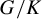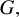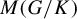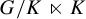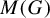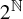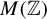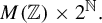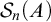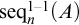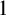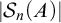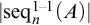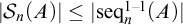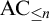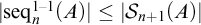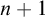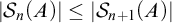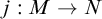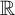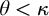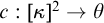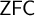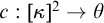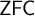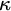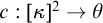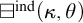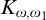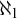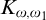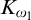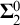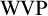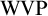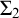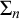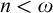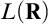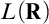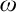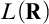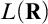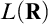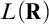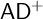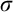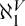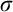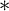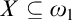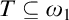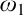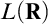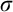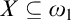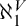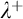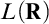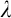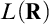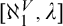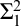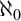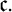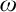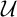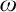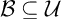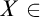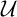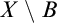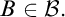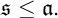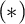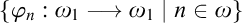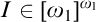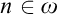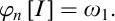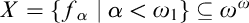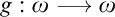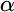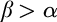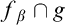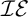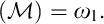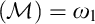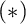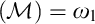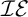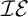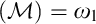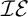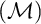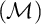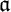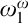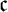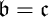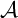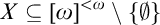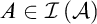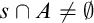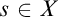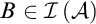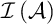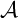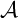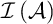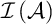The main topics of this thesis are cardinal invariants, P -points and MAD families. Cardinal invariants of the continuum are cardinal numbers that are bigger than 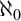 $\aleph _{0}$ and smaller or equal than
$\aleph _{0}$ and smaller or equal than 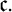 $\mathfrak {c}.$ Of course, they are only interesting when they have some combinatorial or topological definition. An almost disjoint family is a family of infinite subsets of
$\mathfrak {c}.$ Of course, they are only interesting when they have some combinatorial or topological definition. An almost disjoint family is a family of infinite subsets of 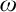 $\omega $ such that the intersection of any two of its elements is finite. A MAD family is a maximal almost disjoint family. An ultrafilter
$\omega $ such that the intersection of any two of its elements is finite. A MAD family is a maximal almost disjoint family. An ultrafilter 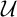 $\mathcal {U}$ on
$\mathcal {U}$ on 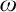 $\omega $ is called a P-point if every countable
$\omega $ is called a P-point if every countable 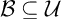 $\mathcal {B\subseteq U}$ there is
$\mathcal {B\subseteq U}$ there is 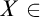 $X\in $
$X\in $ 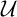 $\mathcal {U}$ such that
$\mathcal {U}$ such that 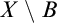 $X\setminus B$ is finite for every
$X\setminus B$ is finite for every 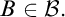 $B\in \mathcal {B}.$ This kind of ultrafilters has been extensively studied, however there is still a large number of open questions about them.
$B\in \mathcal {B}.$ This kind of ultrafilters has been extensively studied, however there is still a large number of open questions about them.
In the preliminaries we recall the principal properties of filters, ultrafilters, ideals, MAD families and cardinal invariants of the continuum. We present the construction of Shelah, Mildenberger, Raghavan, and Steprāns of a completely separable MAD family under 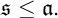 $\mathfrak {s\leq a}.$ None of the results in this chapter are due to the author.
$\mathfrak {s\leq a}.$ None of the results in this chapter are due to the author.
The second chapter is dedicated to a principle of Sierpiński. The principle 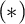 $\left ( \ast \right ) $ of Sierpiński is the following statement: There is a family of functions
$\left ( \ast \right ) $ of Sierpiński is the following statement: There is a family of functions 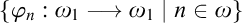 $\left \{ \varphi _{n}:\omega _{1}\longrightarrow \omega _{1}\mid n\in \omega \right \} $ such that for every
$\left \{ \varphi _{n}:\omega _{1}\longrightarrow \omega _{1}\mid n\in \omega \right \} $ such that for every 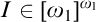 $I\in \left [ \omega _{1}\right ] ^{\omega _{1}}$ there is
$I\in \left [ \omega _{1}\right ] ^{\omega _{1}}$ there is 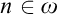 $n\in \omega $ for which
$n\in \omega $ for which 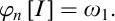 $\varphi _{n}\left [ I\right ] =\omega _{1}.$ This principle was recently studied by Arnie Miller. He showed that this principle is equivalent to the following statement: There is a set
$\varphi _{n}\left [ I\right ] =\omega _{1}.$ This principle was recently studied by Arnie Miller. He showed that this principle is equivalent to the following statement: There is a set 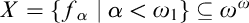 $X=\left \{ f_{\alpha }\mid \alpha <\omega _{1}\right \} \subseteq \omega ^{\omega }$ such that for every
$X=\left \{ f_{\alpha }\mid \alpha <\omega _{1}\right \} \subseteq \omega ^{\omega }$ such that for every 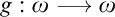 $g:\omega \longrightarrow \omega $ there is
$g:\omega \longrightarrow \omega $ there is 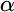 $\alpha $ such that if
$\alpha $ such that if 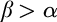 $\beta>\alpha $ then
$\beta>\alpha $ then 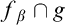 $f_{\beta }\cap g$ is infinite (sets with that property are referred to as
$f_{\beta }\cap g$ is infinite (sets with that property are referred to as 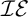 $\mathcal {IE}$-Luzin sets ). Miller showed that the principle of Sierpiński implies that non
$\mathcal {IE}$-Luzin sets ). Miller showed that the principle of Sierpiński implies that non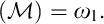 $\left ( \mathcal {M}\right ) =\omega _{1}.$ He asked if the converse was true, i.e., does non
$\left ( \mathcal {M}\right ) =\omega _{1}.$ He asked if the converse was true, i.e., does non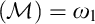 $\left ( \mathcal {M}\right ) =\omega _{1}$ imply the principle
$\left ( \mathcal {M}\right ) =\omega _{1}$ imply the principle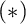 $\left ( \ast \right ) $of Sierpiński? We answer his question affirmatively. In other words, we show that non
$\left ( \ast \right ) $of Sierpiński? We answer his question affirmatively. In other words, we show that non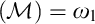 $\left ( \mathcal {M}\right ) =\omega _{1}$ is enough to construct an
$\left ( \mathcal {M}\right ) =\omega _{1}$ is enough to construct an 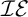 $\mathcal {IE}$-Luzin set. It is not hard to see that the
$\mathcal {IE}$-Luzin set. It is not hard to see that the 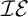 $\mathcal {IE}$-Luzin set we constructed is meager. This is no coincidence, because with the aid of an inaccessible cardinal, we construct a model where non
$\mathcal {IE}$-Luzin set we constructed is meager. This is no coincidence, because with the aid of an inaccessible cardinal, we construct a model where non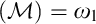 $\left ( \mathcal {M}\right ) =\omega _{1}$ and every
$\left ( \mathcal {M}\right ) =\omega _{1}$ and every 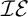 $\mathcal {IE}$-Luzin set is meager.
$\mathcal {IE}$-Luzin set is meager.
The third chapter is dedicated to a conjecture of Hrušák. Michael Hrušák conjectured the following: Every Borel cardinal invariant is either at most non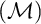 $\left ( \mathcal {M}\right ) $ or at least cov
$\left ( \mathcal {M}\right ) $ or at least cov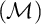 $\left ( \mathcal {M}\right ) $ (it is known that the definability is an important requirement, otherwise
$\left ( \mathcal {M}\right ) $ (it is known that the definability is an important requirement, otherwise 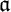 $\mathfrak {a}$ would be a counterexample). Although the veracity of this conjecture is still an open problem, we were able to obtain some partial results: The conjecture is false for “Borel invariants of
$\mathfrak {a}$ would be a counterexample). Although the veracity of this conjecture is still an open problem, we were able to obtain some partial results: The conjecture is false for “Borel invariants of 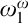 $\omega _{1}^{\omega }$” nevertheless, it is true for a large class of definable invariants. This is part of a joint work with Michael Hrušák and Jindřich Zapletal.
$\omega _{1}^{\omega }$” nevertheless, it is true for a large class of definable invariants. This is part of a joint work with Michael Hrušák and Jindřich Zapletal.
In the fourth chapter we present a survey on destructibility of ideals and MAD families. We prove several classic theorems, but we also prove some new results. For example, we show that every almost disjoint family of size less than 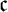 $\mathfrak {c}$ can be extended to a Cohen indestructible MAD family is equivalent to
$\mathfrak {c}$ can be extended to a Cohen indestructible MAD family is equivalent to 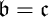 $\mathfrak {b=c}$ (this is part of a joint work with Michael Hrušák, Ariet Ramos, and Carlos Martínez). A MAD family
$\mathfrak {b=c}$ (this is part of a joint work with Michael Hrušák, Ariet Ramos, and Carlos Martínez). A MAD family 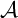 $\mathcal {A}$ is Shelah–Steprāns if for every
$\mathcal {A}$ is Shelah–Steprāns if for every 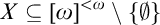 $X\subseteq \left [ \omega \right ] ^{<\omega }\setminus \left \{ \emptyset \right \} $ either there is
$X\subseteq \left [ \omega \right ] ^{<\omega }\setminus \left \{ \emptyset \right \} $ either there is 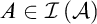 $A\in \mathcal {I}\left ( \mathcal {A}\right ) $ such that
$A\in \mathcal {I}\left ( \mathcal {A}\right ) $ such that 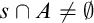 $s\cap A\neq \emptyset $ for every
$s\cap A\neq \emptyset $ for every 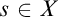 $s\in X$ or there is
$s\in X$ or there is 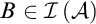 $B\in \mathcal {I}\left ( \mathcal {A}\right ) $ that contains infinitely many elements of X (where
$B\in \mathcal {I}\left ( \mathcal {A}\right ) $ that contains infinitely many elements of X (where 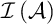 $\mathcal {I}\left ( \mathcal {A}\right ) $ denotes the ideal generated by
$\mathcal {I}\left ( \mathcal {A}\right ) $ denotes the ideal generated by 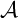 $\mathcal {A}$). This concept was introduced by Raghavan which is connected to the notion of “strongly separable” introduced by Shelah and Steprāns. We prove that Shelah–Steprāns MAD families have very strong indestructibility properties: Shelah–Steprāns MAD families are indestructible for “many” definable forcings that does not add dominating reals (this statement will be formalized in the fourth chapter). According to the author’s best knowledge, this is the strongest notion (in terms of indestructibility) that has been considered in the literature so far. In spite of their strong indestructibility, Shelah–Steprāns MAD families can be destroyed by a ccc forcing that does not add unsplit or dominating reals. We also consider some strong combinatorial properties of MAD families and show the relationships between them (This is part of a joint work with Michael Hrušák, Dilip Raghavan, and Joerg Brendle).
$\mathcal {A}$). This concept was introduced by Raghavan which is connected to the notion of “strongly separable” introduced by Shelah and Steprāns. We prove that Shelah–Steprāns MAD families have very strong indestructibility properties: Shelah–Steprāns MAD families are indestructible for “many” definable forcings that does not add dominating reals (this statement will be formalized in the fourth chapter). According to the author’s best knowledge, this is the strongest notion (in terms of indestructibility) that has been considered in the literature so far. In spite of their strong indestructibility, Shelah–Steprāns MAD families can be destroyed by a ccc forcing that does not add unsplit or dominating reals. We also consider some strong combinatorial properties of MAD families and show the relationships between them (This is part of a joint work with Michael Hrušák, Dilip Raghavan, and Joerg Brendle).
The fifth chapter is one of the most important chapters in the thesis. A MAD family 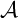 $\mathcal {A}$ is called
$\mathcal {A}$ is called  $+$-Ramsey if every tree that branches into
$+$-Ramsey if every tree that branches into 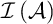 $\mathcal {I}\left ( \mathcal {A}\right ) $-positive sets has an
$\mathcal {I}\left ( \mathcal {A}\right ) $-positive sets has an 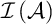 $\mathcal {I}\left ( \mathcal {A}\right ) $-positive branch. Michael Hrušák’s first published question is the following: Is there a
$\mathcal {I}\left ( \mathcal {A}\right ) $-positive branch. Michael Hrušák’s first published question is the following: Is there a  $+$-Ramsey MAD family? It was previously known that such families can consistently exist. However, there was no construction of such families using only the axioms of ZFC. We solve this problem by constructing such a family without any extra assumptions.
$+$-Ramsey MAD family? It was previously known that such families can consistently exist. However, there was no construction of such families using only the axioms of ZFC. We solve this problem by constructing such a family without any extra assumptions.
In the fourth and fifth chapters, we introduce several notions of MAD families, in the sixth chapter we prove several implications and non implications between them. We construct (under  $\mathsf {CH}$) several MAD families with different properties.
$\mathsf {CH}$) several MAD families with different properties.
In the seventh chapter we build models without P -points. We show that there are no P -points after adding Silver reals either iteratively or by the side by side product. These results have some important consequences: The first one is that is its possible to get rid of P -points using only definable forcings. This answers a question of Michael Hrušák. We can also use our results to build models with no P -points and with arbitrarily large continuum, which was also an open question. These results were obtained with David Chodounský.
Abstract prepared by Osvaldo Guzmán González
E-mail : oguzman@matmor.unam.mx
URL : https://arxiv.org/abs/1810.09680
 $\mathrm {NF}$
$\mathrm {NF}$
 $\omega _1$
$\omega _1$
 $ K_{\omega _1}$ AND
$ K_{\omega _1}$ AND  $K_{\omega ,\omega _1}$
$K_{\omega ,\omega _1}$