In this paper we consider systems of diagonal forms with integer coefficients in which each form has a different degree. Every such system has a nontrivial zero in every p-adic field Qp provided that the number of variables is sufficiently large in terms of the degrees. While the number of variables required grows at least exponentially as the degrees and number of forms increase, it is known that if p is sufficiently large then only a small polynomial bound is required to ensure zeros in Qp. In this paper we explore the question of how small we can make the prime p and still have a polynomial bound. In particular, we show that we may allow p to be smaller than the largest of the degrees.

A geometric mass concerning supersingular abelian varieties with real multiplications is formulated and related to an arithmetic mass. We determine the exact geometric mass formula for superspecial abelian varieties of Hubert-Blumenthal type. As an application, we compute the number of the irreducible components of the supersingular locus of some Hubert-Blumenthal varieties in terms of special values of the zeta function.

A positive definite integral quadratic form over rational integers is said to be universal, if it represents all positive integers. The universal quaternary quadratic form is determined with the maximal discriminant, which is 1073/4.

We continue our study of the different representations of an integer n as a sum of two squares initiated in our final paper written with Paul Erdős [1]. We let r(n) denote the number of representations n = a2 + b2 counted in the usual way, that is, with regard to both the order and sign of a and b. We have

where x is the non-principal Dirichlet character (mod 4); moreover, r(n)≥0 if and only if n has no prime factor p ≡ 3 (mod 4) with odd exponent. We define the function b(n) on the sequence of representable numbers as the least possible value of |b|—for example, we have b(13) = 2,b(25) = 0, b(65) = 1—and we write

here and throughout the paper the star denotes that the sum is restricted to the representable integers. The problem considered here is to find an asymptotic formula for this sum, or, less ambitiously, to determine the order of magnitude of the function B(x).

In this paper we prove that every positive definite n-ary integral quadratic form with 12 < n < 13 (respectively 14 ≦ n ≤ 20) that can be represented by a sum of squares of integral linear forms is represented by a sum of 2 · 3n + n + 6 (respectively 3 · 4n + n + 3) squares. We also prove that every positive definite 7-ary integral quadratic form that can be represented by a sum of squares is represented by a sum of 25 squares.

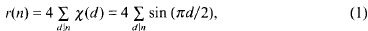
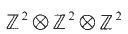The space of integral 3-tensors is under the standard action of 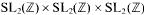. A notion of primitivity is defined in this space and the number of primitive classes of a given discriminant is evaluated in terms of the class number of primitive binary quadratic forms of the same discriminant. Classes containing symmetric 3-tensors are also considered and their number is related to the 3-rank of the class group.

Suppose we are given a regular symmetric bilinear from on a finite-dimensional vector space V over a commutative field K of characteristic ≠ 2. We want to write given elements of the commutator subgroup ω(V) (of the orthogonal group O(V)) and also of the kernel of the spinorial norm ker(Θ) as (short) products of involutions and as products of commutators

Let K be a nonarchimedean local field, let L be a separable quadratic extension of K, and let h denote a nondegenerate sesquilinear formk on L3. The Bruhat-Tits building associated with SU3(h) is a tree. This is applied to the study of certain groups acting simply transitively on vertices of the building associated with SL(3, F), F = Q3 or F3((X)).

In [CKR], Chan, Kim and Raghavan determine all universal positive ternary integral quadratic forms over real quadratic number fields. In this context, universal means that the form represents all totally positive elements of the ring of integers of the underlying field. This generalizes the usage of the term introduced by Dickson for the case of the ring of rational integers [D]. In the present paper, we will continue the investigation of quadratic forms with this property, considering positive quaternary forms over totally real number fields. The main goal of the paper is to prove that if E is a totally real number field of odd degree over the field of rational numbers, then there are at most finitely many inequivalent universal positive quaternary quadratic forms over the ring of integers of E. In fact, the stronger result will be proved that this finiteness holds for those forms which represent all totally positive multiples of any fixed totally positive integer. The necessity of the assumption of oddness of the degree of the extension for a general result of this type can be seen from the existence of universal ternary forms over certain real quadratic fields (for example, the sum of three squares over the field ℚ(√5), as first shown by Maass [M]).

In the paper [2] Hsia noted that the forms x2+xy+y2+9z2 and x2+3y2+3yz+3z2 constitute a genus and that both forms are regular; he asked whether there exist any other genera containing two or more regular forms. In this note it is proved that the forms

are regular. They constitute a genus with discriminant 27 (in the normalization used by Brandt and Intrau in [1]). It is noteworthy that Hsia's genus has the same discriminant.

John Conway's analysis in 1968 of the automorphism group of the Leech lattice and his discovery of three sporadic simple groups led to the immediate speculation that other Z-lattices might have interesting automorphism groups which give rise to (possibly new) finite simple groups. (The classification theorem for the finite simple groups has since told us that no new finite simple groups can arise in this or any other way.) For example in 1973, M. Broué and M. Enguehard constructed, in every dimension 2n, an even lattice (unimodular if n is odd) whose automorphism group is related to the simple Chevalley group of type Dn. This family of integral lattices received attention and acclaim in the subsequent literature. What escaped the attention of this literature, however, was the fact that these lattices had been discovered years earlier. Indeed in 1959, E. S. Barnes and G. E. Wall gave a uniform construction for a large class of positive definite Z-lattices in dimensions 2n which include those of Broué and Enguehard as special cases. The present article introduces an abstracted and generalized version of the construction of Barnes and Wall. In addition, there are some new observations about Barnes-Wall lattices. In particular, it is shown how to associate to each such lattice a continuous, piecewise linear graph in the plane from which all the important properties of the lattice, for example, its minimum, whether it is integral, unimodular, even, or perfect can be read off directly.