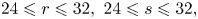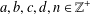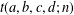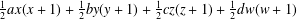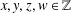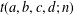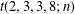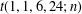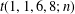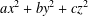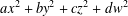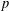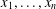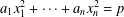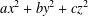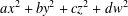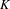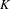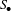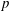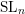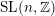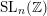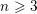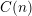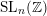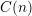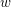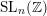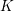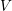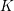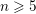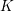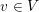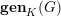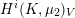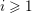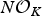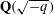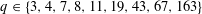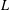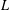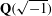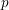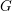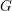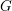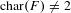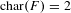Refine listing
Actions for selected content:
114 results in 11Exx
Nonsingular bilinear maps revisited
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 17 March 2020, pp. 377-390
- Print publication:
- February 2021
-
- Article
- Export citation
APPLICATIONS OF SYSTEMS OF QUADRATIC FORMS TO GENERALISED QUADRATIC FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 13 February 2020, pp. 374-386
- Print publication:
- December 2020
-
- Article
- Export citation
TRANSFORMATION FORMULAS FOR THE NUMBER OF REPRESENTATIONS OF
 $n$ BY LINEAR COMBINATIONS OF FOUR TRIANGULAR NUMBERS
$n$ BY LINEAR COMBINATIONS OF FOUR TRIANGULAR NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 39-49
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Patching over Berkovich curves and quadratic forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 12 / December 2019
- Published online by Cambridge University Press:
- 11 November 2019, pp. 2399-2438
- Print publication:
- December 2019
-
- Article
- Export citation
PRIME-UNIVERSAL QUADRATIC FORMS
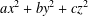 $ax^{2}+by^{2}+cz^{2}$ AND
$ax^{2}+by^{2}+cz^{2}$ AND 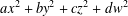 $ax^{2}+by^{2}+cz^{2}+dw^{2}$
$ax^{2}+by^{2}+cz^{2}+dw^{2}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 27 September 2019, pp. 1-12
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
HIGHER
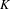 $K$-THEORY OF FORMS I. FROM RINGS TO EXACT CATEGORIES
$K$-THEORY OF FORMS I. FROM RINGS TO EXACT CATEGORIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 4 / July 2021
- Published online by Cambridge University Press:
- 02 August 2019, pp. 1205-1273
- Print publication:
- July 2021
-
- Article
- Export citation
Retract Rationality and Algebraic Tori
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 18 July 2019, pp. 173-186
- Print publication:
- March 2020
-
- Article
-
- You have access
- Export citation
Affine quadrics and the Picard group of the motivic category
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 8 / August 2019
- Published online by Cambridge University Press:
- 04 July 2019, pp. 1500-1520
- Print publication:
- August 2019
-
- Article
- Export citation
Le principe de Hasse pour les espaces homogènes : réduction au cas des stabilisateurs finis
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 8 / August 2019
- Published online by Cambridge University Press:
- 04 July 2019, pp. 1568-1593
- Print publication:
- August 2019
-
- Article
- Export citation
Words have bounded width in
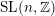 $\operatorname{SL}(n,\mathbb{Z})$
$\operatorname{SL}(n,\mathbb{Z})$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 7 / July 2019
- Published online by Cambridge University Press:
- 13 June 2019, pp. 1245-1258
- Print publication:
- July 2019
-
- Article
- Export citation
Autoequivalences of twisted K3 surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 5 / May 2019
- Published online by Cambridge University Press:
- 30 April 2019, pp. 912-937
- Print publication:
- May 2019
-
- Article
- Export citation
Spinor groups with good reduction
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 3 / March 2019
- Published online by Cambridge University Press:
- 07 March 2019, pp. 484-527
- Print publication:
- March 2019
-
- Article
- Export citation
Binary quadratic forms and ray class groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 23 January 2019, pp. 695-720
- Print publication:
- April 2020
-
- Article
- Export citation
CLASS NUMBER ONE FROM ANALYTIC RANK TWO
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 2 / 2019
- Published online by Cambridge University Press:
- 03 January 2019, pp. 333-374
- Print publication:
- 2019
-
- Article
- Export citation
INTERVALS BETWEEN CONSECUTIVE NUMBERS WHICH ARE SUMS OF TWO SQUARES
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 4 / 2019
- Published online by Cambridge University Press:
- 14 August 2019, pp. 1018-1032
- Print publication:
- 2019
-
- Article
- Export citation
COMPLETENESS OF THE LIST OF SPINOR REGULAR TERNARY QUADRATIC FORMS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 2 / 2019
- Published online by Cambridge University Press:
- 05 December 2018, pp. 213-235
- Print publication:
- 2019
-
- Article
- Export citation
On the Frequency of Algebraic Brauer Classes on Certain Log K3 Surfaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 03 December 2018, pp. 551-563
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
INTERTWINING SEMISIMPLE CHARACTERS FOR
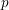 $p$-ADIC CLASSICAL GROUPS
$p$-ADIC CLASSICAL GROUPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 238 / June 2020
- Published online by Cambridge University Press:
- 16 July 2018, pp. 137-205
- Print publication:
- June 2020
-
- Article
-
- You have access
- HTML
- Export citation
COMMON SLOTS OF BILINEAR AND QUADRATIC PFISTER FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 03 May 2018, pp. 38-47
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
A BOUND FOR THE INDEX OF A QUADRATIC FORM AFTER SCALAR EXTENSION TO THE FUNCTION FIELD OF A QUADRIC
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 16 April 2018, pp. 421-450
- Print publication:
- March 2020
-
- Article
- Export citation