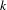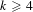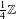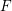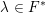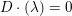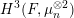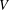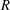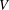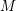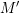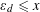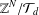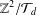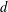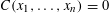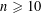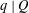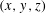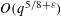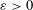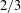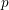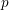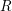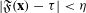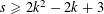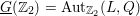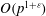Refine listing
Actions for selected content:
114 results in 11Exx
Sums of three squares and Noether–Lefschetz loci
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 5 / May 2018
- Published online by Cambridge University Press:
- 03 April 2018, pp. 1048-1065
- Print publication:
- May 2018
-
- Article
- Export citation
EPSTEIN ZETA-FUNCTIONS, SUBCONVEXITY, AND THE PURITY CONJECTURE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 02 April 2018, pp. 581-596
- Print publication:
- March 2020
-
- Article
- Export citation
Local–global principle for reduced norms over function fields of
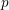 $p$ -adic curves
$p$ -adic curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 2 / February 2018
- Published online by Cambridge University Press:
- 02 November 2017, pp. 410-458
- Print publication:
- February 2018
-
- Article
- Export citation
SYMMETRIC SQUARE-CENTRAL ELEMENTS IN PRODUCTS OF ORTHOGONAL INVOLUTIONS IN CHARACTERISTIC TWO
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 17 August 2017, pp. 412-425
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
CONGRUENCE OF SYMMETRIC INNER PRODUCTS OVER FINITE COMMUTATIVE RINGS OF ODD CHARACTERISTIC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 08 June 2017, pp. 389-397
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
Construction of automorphisms of hyperkähler manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 8 / August 2017
- Published online by Cambridge University Press:
- 31 May 2017, pp. 1610-1621
- Print publication:
- August 2017
-
- Article
- Export citation
Spinors and essential dimension
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 3 / March 2017
- Published online by Cambridge University Press:
- 02 March 2017, pp. 535-556
- Print publication:
- March 2017
-
- Article
- Export citation
Picard curves over
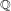 $\mathbb{Q}$ with good reduction away from 3
$\mathbb{Q}$ with good reduction away from 3
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 01 March 2017, pp. 382-408
-
- Article
-
- You have access
- Export citation
LARGE MOMENTS AND EXTREME VALUES OF CLASS NUMBERS OF INDEFINITE BINARY QUADRATIC FORMS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 20 April 2017, pp. 564-586
- Print publication:
- 2017
-
- Article
- Export citation
ALGEBRAIC AND GEOMETRIC PROPERTIES OF LATTICE WALKS WITH STEPS OF EQUAL LENGTH
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 02 November 2016, pp. 338-346
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
UNIVERSAL QUADRATIC FORMS AND ELEMENTS OF SMALL NORM IN REAL QUADRATIC FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 11 January 2016, pp. 7-14
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
RATIONAL POINTS ON CUBIC HYPERSURFACES THAT SPLIT INTO FOUR FORMS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 29 January 2016, pp. 430-440
- Print publication:
- 2016
-
- Article
- Export citation
SMALL SOLUTIONS OF QUADRATIC CONGRUENCES, AND CHARACTER SUMS WITH BINARY QUADRATIC FORMS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 18 February 2016, pp. 551-571
- Print publication:
- 2016
-
- Article
- Export citation
The pro-
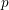 $p$-Iwahori Hecke algebra of a reductive
$p$-Iwahori Hecke algebra of a reductive 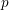 $p$-adic group I
$p$-adic group I
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 23 October 2015, pp. 693-753
- Print publication:
- April 2016
-
- Article
- Export citation
Invariants of degree 3 and torsion in the Chow group of a versal flag
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 8 / August 2015
- Published online by Cambridge University Press:
- 16 April 2015, pp. 1416-1432
- Print publication:
- August 2015
-
- Article
- Export citation
WARING’S PROBLEM WITH SHIFTS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 06 March 2015, pp. 13-46
- Print publication:
- 2016
-
- Article
- Export citation
REPRESENTATIONS OF ALTERNATIVE CLIFFORD ALGEBRAS OF QUADRATIC FORMS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 18 December 2014, pp. 579-590
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
ADVENTURES IN INVARIANT THEORY
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 56 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 15 December 2014, pp. 105-115
-
- Article
-
- You have access
- Export citation
Group schemes and local densities of quadratic lattices in residue characteristic 2
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 5 / May 2015
- Published online by Cambridge University Press:
- 05 December 2014, pp. 793-827
- Print publication:
- May 2015
-
- Article
- Export citation
Constructing supersingular elliptic curves with a given endomorphism ring
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 71-91
-
- Article
-
- You have access
- Export citation