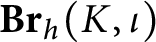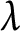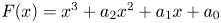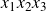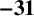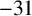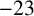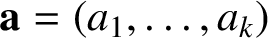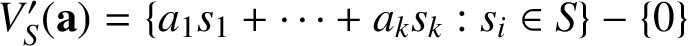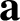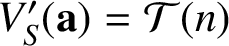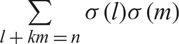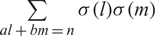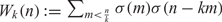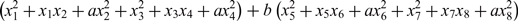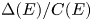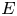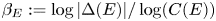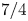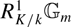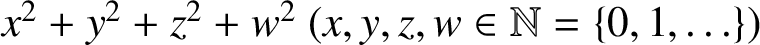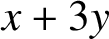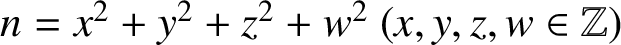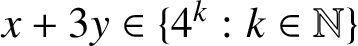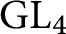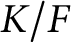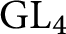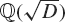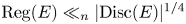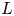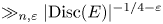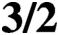Refine listing
Actions for selected content:
114 results in 11Exx
Mixed Witt rings of algebras with involution
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 29 March 2022, pp. 608-644
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On monic abelian cubics
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 16 May 2022, pp. 550-567
- Print publication:
- March 2022
-
- Article
- Export citation
Uniform bounds for norms of theta series and arithmetic applications
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 28 February 2022, pp. 669-691
- Print publication:
- November 2022
-
- Article
- Export citation
AN APPLICATION OF BINARY QUADRATIC FORMS OF DISCRIMINANT
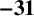 $\boldsymbol {-31}$ TO MODULAR FORMS
$\boldsymbol {-31}$ TO MODULAR FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 269-272
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TIGHT UNIVERSAL TRIANGULAR FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 18 November 2021, pp. 372-384
- Print publication:
- June 2022
-
- Article
- Export citation
THE BOREL CHARACTER
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 26 July 2021, pp. 747-797
- Print publication:
- March 2023
-
- Article
- Export citation
EVALUATION OF CONVOLUTION SUMS
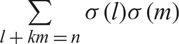 $$\sum\limits_{l + km = n} {\sigma (l)\sigma (m)} $$ AND
$$\sum\limits_{l + km = n} {\sigma (l)\sigma (m)} $$ AND 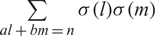 $$\sum\limits_{al + bm = n} {\sigma (l)\sigma (m)} $$ FOR k = a · b = 21, 33, AND 35
$$\sum\limits_{al + bm = n} {\sigma (l)\sigma (m)} $$ FOR k = a · b = 21, 33, AND 35
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 16 July 2021, pp. 434-453
- Print publication:
- May 2022
-
- Article
- Export citation
Counting and equidistribution in quaternionic Heisenberg groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 1 / July 2022
- Published online by Cambridge University Press:
- 08 July 2021, pp. 67-104
- Print publication:
- July 2022
-
- Article
- Export citation
Large families of elliptic curves ordered by conductor
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 22 June 2021, pp. 1538-1583
- Print publication:
- July 2021
-
- Article
- Export citation
Explicit methods for the Hasse norm principle and applications to An and Sn extensions
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 22 April 2021, pp. 489-529
- Print publication:
- May 2022
-
- Article
-
- You have access
- Open access
- Export citation
NONNEGATIVE POLYNOMIALS, SUMS OF SQUARES AND THE MOMENT PROBLEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 19 February 2021, pp. 337-341
- Print publication:
- October 2021
-
- Article
-
- You have access
- Export citation
SUMS OF FOUR SQUARES WITH A CERTAIN RESTRICTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 14 January 2021, pp. 218-227
- Print publication:
- October 2021
-
- Article
- Export citation
A proof of the linear Arithmetic Fundamental Lemma for
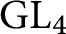 $ \operatorname {{\mathrm {GL}}}_4$
$ \operatorname {{\mathrm {GL}}}_4$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 23 November 2020, pp. 381-427
- Print publication:
- April 2022
-
- Article
- Export citation
Zeros of the Epstein zeta function to the right of the critical line
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 2 / September 2021
- Published online by Cambridge University Press:
- 17 November 2020, pp. 265-276
- Print publication:
- September 2021
-
- Article
- Export citation
Non-vanishing of class group L-functions for number fields with a small regulator
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 17 December 2020, pp. 2423-2436
- Print publication:
- November 2020
-
- Article
- Export citation
CONGRUENCES MODULO 4 FOR WEIGHT
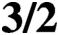 $\textbf{3/2}$ ETA-PRODUCTS
$\textbf{3/2}$ ETA-PRODUCTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 05 October 2020, pp. 405-417
- Print publication:
- June 2021
-
- Article
- Export citation
PRIME-UNIVERSAL DIAGONAL QUADRATIC FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 05 October 2020, pp. 390-404
- Print publication:
- June 2021
-
- Article
- Export citation
There are no universal ternary quadratic forms over biquadratic fields
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 3 / August 2020
- Published online by Cambridge University Press:
- 16 September 2020, pp. 861-912
-
- Article
- Export citation
NONBINARY DELSARTE–GOETHALS CODES AND FINITE SEMIFIELDS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue S1 / December 2020
- Published online by Cambridge University Press:
- 07 May 2020, pp. S186-S205
- Print publication:
- December 2020
-
- Article
- Export citation
Rational lines on cubic hypersurfaces
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 1 / July 2021
- Published online by Cambridge University Press:
- 24 April 2020, pp. 99-112
- Print publication:
- July 2021
-
- Article
-
- You have access
- Open access
- Export citation