Refine listing
Actions for selected content:
186 results in 11Kxx
Slice discrepancy and irregularities of distribution on spheres
- Part of
-
- Journal:
- Mathematika / Volume 38 / Issue 1 / June 1991
- Published online by Cambridge University Press:
- 26 February 2010, pp. 105-116
- Print publication:
- June 1991
-
- Article
- Export citation
Normality of some p—adic product expansions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 2 / October 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 258-263
- Print publication:
- October 1990
-
- Article
-
- You have access
- Export citation
Notes on uniform distribution modulo one
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 2 / October 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 264-272
- Print publication:
- October 1990
-
- Article
-
- You have access
- Export citation
On the product of distances to a point set on a sphere
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 3 / December 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 466-482
- Print publication:
- December 1989
-
- Article
-
- You have access
- Export citation
The Hausdorff Dimension of a Set of Normal Numbers II
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 44 / Issue 2 / April 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 259-264
- Print publication:
- April 1988
-
- Article
-
- You have access
- Export citation
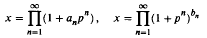
 and, for the variable point
and, for the variable point  from
from 
















