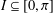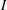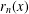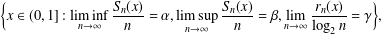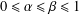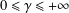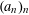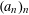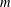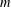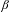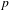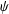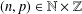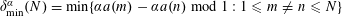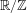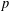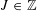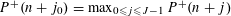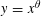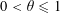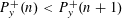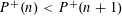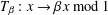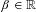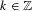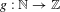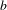Refine listing
Actions for selected content:
182 results in 11Kxx
THE ERROR TERM IN THE SATO–TATE THEOREM OF BIRCH
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 08 February 2019, pp. 27-33
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
A NOTE ON THE INTERSECTIONS OF THE BESICOVITCH SETS AND ERDŐS–RÉNYI SETS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 01 February 2019, pp. 33-45
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
On the geometry and regularity of invariant sets of piecewise-affine automorphisms on the Euclidean space
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 07 January 2019, pp. 2183-2218
- Print publication:
- August 2020
-
- Article
- Export citation
THERE IS NO KHINTCHINE THRESHOLD FOR METRIC PAIR CORRELATIONS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 4 / 2019
- Published online by Cambridge University Press:
- 23 July 2019, pp. 929-949
- Print publication:
- 2019
-
- Article
- Export citation
POINT DISTRIBUTIONS IN TWO-POINT HOMOGENEOUS SPACES
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 26 March 2019, pp. 557-587
- Print publication:
- 2019
-
- Article
- Export citation
RANDOMNESS AND NON-RANDOMNESS PROPERTIES OF PIATETSKI-SHAPIRO SEQUENCES MODULO
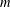 $m$
$m$
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 4 / 2019
- Published online by Cambridge University Press:
- 14 August 2019, pp. 1051-1073
- Print publication:
- 2019
-
- Article
- Export citation
LONELY RUNNERS IN FUNCTION FIELDS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 12 April 2019, pp. 677-701
- Print publication:
- 2019
-
- Article
- Export citation
Digit frequencies and self-affine sets with non-empty interior
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 19 December 2018, pp. 1755-1787
- Print publication:
- July 2020
-
- Article
- Export citation
Metrical Results on the Distribution of Fractional Parts of Powers of Real Numbers
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 29 November 2018, pp. 505-521
-
- Article
- Export citation
SOME REFINED RESULTS ON THE MIXED LITTLEWOOD CONJECTURE FOR PSEUDO-ABSOLUTE VALUES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 22 August 2018, pp. 91-109
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
A mass transference principle for systems of linear forms and its applications
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 5 / May 2018
- Published online by Cambridge University Press:
- 03 April 2018, pp. 1014-1047
- Print publication:
- May 2018
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Quantitative Metric Theory of Continued Fractions in Positive Characteristic
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 07 February 2018, pp. 283-293
-
- Article
-
- You have access
- Open access
- Export citation
HAUSDORFF DIMENSION OF THE SET APPROXIMATED BY IRRATIONAL ROTATIONS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 14 February 2018, pp. 267-283
- Print publication:
- 2018
-
- Article
- Export citation
HAUSDORFF MEASURE OF SETS OF DIRICHLET NON-IMPROVABLE NUMBERS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 19 April 2018, pp. 502-518
- Print publication:
- 2018
-
- Article
- Export citation
A METRIC THEORY OF MINIMAL GAPS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 3 / 2018
- Published online by Cambridge University Press:
- 21 May 2018, pp. 628-636
- Print publication:
- 2018
-
- Article
- Export citation
WEAK ADMISSIBILITY, PRIMITIVITY, O-MINIMALITY, AND DIOPHANTINE APPROXIMATION
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 17 April 2018, pp. 475-496
- Print publication:
- 2018
-
- Article
- Export citation
THE PRIMES ARE NOT METRIC POISSONIAN
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 14 February 2018, pp. 230-236
- Print publication:
- 2018
-
- Article
- Export citation
SUR LES PLUS GRANDS FACTEURS PREMIERSD’ENTIERS CONSÉCUTIFS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 05 April 2018, pp. 343-379
- Print publication:
- 2018
-
- Article
- Export citation
TWO-DIMENSIONAL SHRINKING TARGET PROBLEM IN BETA-DYNAMICAL SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 02 November 2017, pp. 33-42
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
PROPRIÉTÉS LOCALES DES CHIFFRES DES NOMBRES PREMIERS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 04 April 2017, pp. 189-224
- Print publication:
- January 2019
-
- Article
- Export citation