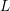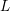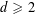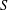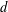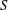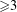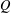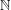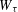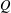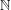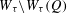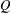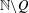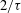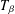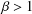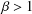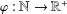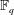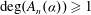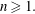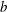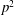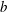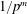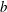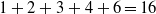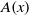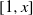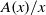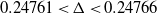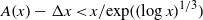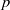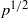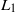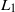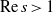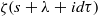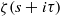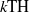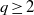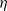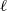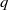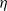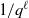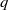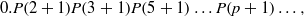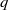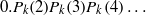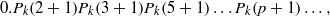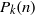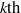Refine listing
Actions for selected content:
182 results in 11Kxx
Diophantine properties of nilpotent Lie groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 6 / June 2015
- Published online by Cambridge University Press:
- 13 January 2015, pp. 1157-1188
- Print publication:
- June 2015
-
- Article
- Export citation
Effective limit distribution of the Frobenius numbers
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 5 / May 2015
- Published online by Cambridge University Press:
- 22 December 2014, pp. 898-916
- Print publication:
- May 2015
-
- Article
- Export citation
A Frostman-Type Lemma for Sets with Large Intersections, and an Application to Diophantine Approximation
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 27 October 2014, pp. 521-542
-
- Article
-
- You have access
- Export citation
Unnormalized differences between zeros of L-functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 2 / February 2015
- Published online by Cambridge University Press:
- 24 October 2014, pp. 230-252
- Print publication:
- February 2015
-
- Article
- Export citation
FROM KHINCHIN’S CONJECTURE ON STRONG UNIFORMITY TO SUPERUNIFORM MOTIONS
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 20 October 2014, pp. 591-707
- Print publication:
- September 2015
-
- Article
- Export citation
HAUSDORFF DIMENSIONS OF SOME LIMINF SETS IN DIOPHANTINE APPROXIMATION
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 17 September 2014, pp. 101-120
- Print publication:
- January 2015
-
- Article
- Export citation
A NOTE ON INHOMOGENEOUS DIOPHANTINE APPROXIMATION IN BETA-DYNAMICAL SYSTEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 12 September 2014, pp. 34-40
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
Metric Diophantine approximation on homogeneous varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 8 / August 2014
- Published online by Cambridge University Press:
- 20 June 2014, pp. 1435-1456
- Print publication:
- August 2014
-
- Article
- Export citation
On the beta expansion of Salem numbers of degree 8
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 June 2014, pp. 289-301
-
- Article
-
- You have access
- Export citation
ON THE METRIC THEORY OF CONTINUED FRACTIONS IN POSITIVE CHARACTERISTIC
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 2 / July 2014
- Published online by Cambridge University Press:
- 27 May 2014, pp. 307-320
- Print publication:
- July 2014
-
- Article
-
- You have access
- Export citation
AN ARITHMETICAL EXCURSION VIA STONEHAM NUMBERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 27 March 2014, pp. 303-315
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Random Construction of Interpolating Sets for High-Dimensional Integration
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 1 / March 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 92-105
- Print publication:
- March 2014
-
- Article
-
- You have access
- Export citation
THE ERROR TERM IN THE COUNT OF ABUNDANT NUMBERS
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 02 January 2014, pp. 43-65
- Print publication:
- January 2014
-
- Article
- Export citation
ON SOLUTIONS TO SOME POLYNOMIAL CONGRUENCES IN SMALL BOXES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 07 August 2013, pp. 300-307
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
SOLUTIONS TO POLYNOMIAL CONGRUENCES IN WELL-SHAPED SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 12 June 2013, pp. 435-447
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
A defect relation for meromorphic maps on generalized p-parabolic manifolds intersecting hypersurfaces in complex projective algebraic varieties
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 21 March 2013, pp. 551-574
-
- Article
-
- You have access
- Export citation
LOWER BOUNDS FOR
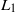 ${L}_{1} $ DISCREPANCY
${L}_{1} $ DISCREPANCY
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 2 / July 2013
- Published online by Cambridge University Press:
- 18 March 2013, pp. 365-379
- Print publication:
- July 2013
-
- Article
- Export citation
A NOTE ON THE HAUSDORFF DIMENSION OF SOME LIMINF SETS APPEARING IN SIMULTANEOUS DIOPHANTINE APPROXIMATION
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 05 December 2012, pp. 56-64
- Print publication:
- January 2013
-
- Article
- Export citation
SELF-APPROXIMATION FOR THE RIEMANN ZETA FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 31 October 2012, pp. 452-461
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
CONSTRUCTION OF NORMAL NUMBERS USING THE DISTRIBUTION OF THE
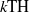 $k\rm TH$ LARGEST PRIME FACTOR
$k\rm TH$ LARGEST PRIME FACTOR
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 31 October 2012, pp. 158-168
- Print publication:
- August 2013
-
- Article
-
- You have access
- Export citation
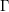
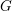
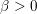
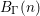
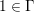
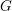
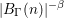
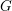
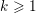
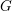
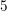
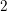
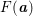

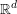


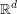
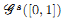 of subsets of [0, 1], originally introduced by Falconer, that are closed under countable intersections, and such that every set in the class has Hausdorff dimension at least
of subsets of [0, 1], originally introduced by Falconer, that are closed under countable intersections, and such that every set in the class has Hausdorff dimension at least 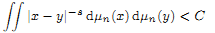
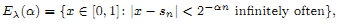
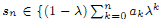 and
and 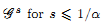 . This improves one of our previously published results.
. This improves one of our previously published results.