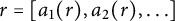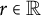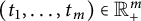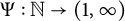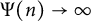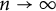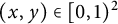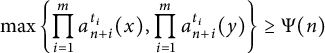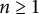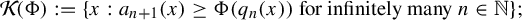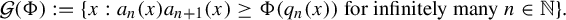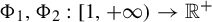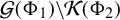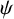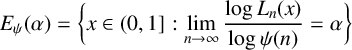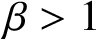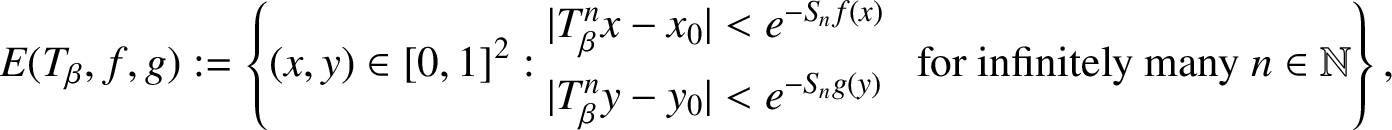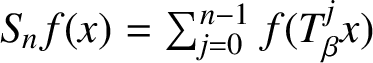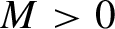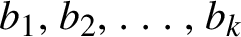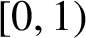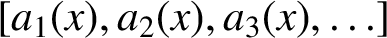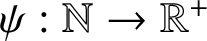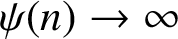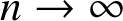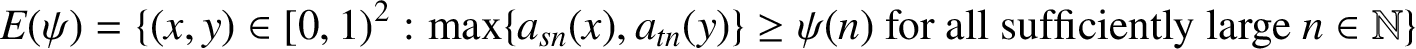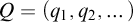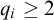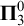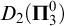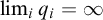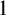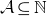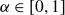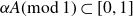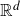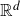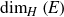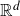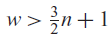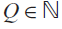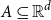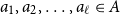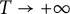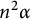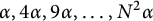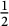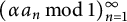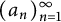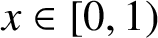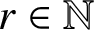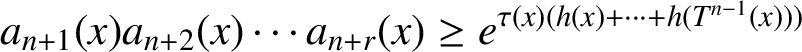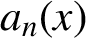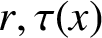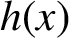Refine listing
Actions for selected content:
186 results in 11Kxx
A note on the relative growth of products of multiple partial quotients in the plane
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 19 August 2022, pp. 544-552
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hausdorff dimension of Dirichlet non-improvable set versus well-approximable set
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 8 / August 2023
- Published online by Cambridge University Press:
- 04 August 2022, pp. 2707-2731
- Print publication:
- August 2023
-
- Article
- Export citation
ON LÜROTH EXPANSIONS IN WHICH THE LARGEST DIGIT GROWS WITH SLOWLY INCREASING SPEED
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 23 June 2022, pp. 204-214
- Print publication:
- April 2023
-
- Article
- Export citation
Ergodicity of Iwasawa continued fractions via markable hyperbolic geodesics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 28 March 2022, pp. 1666-1711
- Print publication:
- May 2023
-
- Article
- Export citation
HIGHER-DIMENSIONAL SHRINKING TARGET PROBLEM FOR BETA DYNAMICAL SYSTEMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 22 March 2022, pp. 289-311
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RETRACTED - THE KRONECKER–WEYL EQUIDISTRIBUTION THEOREM AND GEODESICS IN 3-MANIFOLDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 21 March 2022, pp. 1-44
-
- Article
- Export citation
Fractal projections with an application in number theory
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 16 March 2022, pp. 1760-1784
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sums of random multiplicative functions over function fields with few irreducible factors
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 28 February 2022, pp. 715-726
- Print publication:
- November 2022
-
- Article
- Export citation
Hausdorff dimension of the set of almost convergent sequences
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 06 January 2022, pp. 691-697
- Print publication:
- September 2022
-
- Article
- Export citation
ON THE INCREASING PARTIAL QUOTIENTS OF CONTINUED FRACTIONS OF POINTS IN THE PLANE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 17 December 2021, pp. 404-411
- Print publication:
- June 2022
-
- Article
- Export citation
A DIMENSIONAL RESULT ON THE PRODUCT OF CONSECUTIVE PARTIAL QUOTIENTS IN CONTINUED FRACTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 11 October 2021, pp. 357-385
- Print publication:
- December 2022
-
- Article
- Export citation
DESCRIPTIVE COMPLEXITY IN CANTOR SERIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 27 September 2021, pp. 1023-1045
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Remarks about inhomogeneous pair correlations
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 2 / September 2022
- Published online by Cambridge University Press:
- 06 September 2021, pp. 369-386
- Print publication:
- September 2022
-
- Article
- Export citation
METRICAL PROBLEMS IN DIOPHANTINE APPROXIMATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 26 July 2021, pp. 519-521
- Print publication:
- December 2021
-
- Article
-
- You have access
- HTML
- Export citation
Random fractals and their intersection with winning sets
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 07 July 2021, pp. 655-684
- Print publication:
- May 2022
-
- Article
- Export citation
QUANTITATIVE ESTIMATE FOR THE MEASURE OF A SET OF REAL NUMBERS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 06 July 2021, pp. 411-433
- Print publication:
- May 2022
-
- Article
- Export citation
On convex holes in d-dimensional point sets
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 18 June 2021, pp. 101-108
-
- Article
- Export citation
On the distribution of the digits of quotients of integers and primes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 279-295
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the triple correlations of fractional parts of
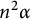 $n^2\alpha $
$n^2\alpha $
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 04 May 2021, pp. 1347-1384
- Print publication:
- October 2022
-
- Article
- Export citation
HAUSDORFF DIMENSION FOR THE SET OF POINTS CONNECTED WITH THE GENERALIZED JARNÍK–BESICOVITCH SET
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 07 December 2020, pp. 1-29
- Print publication:
- February 2022
-
- Article
- Export citation