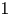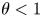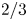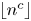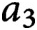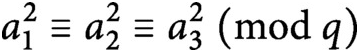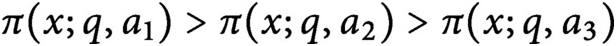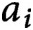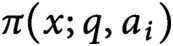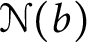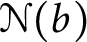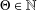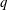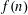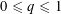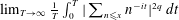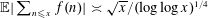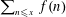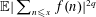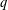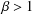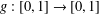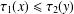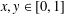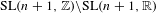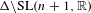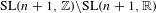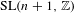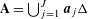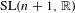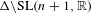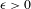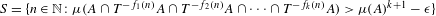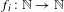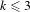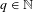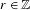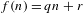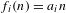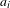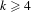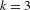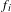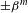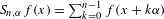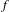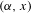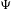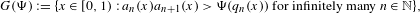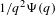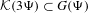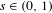Refine listing
Actions for selected content:
186 results in 11Kxx
Sarnak’s conjecture for sequences of almost quadratic word growth
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 04 December 2020, pp. 3060-3115
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- Export citation
The level of distribution of the Thue–Morse sequence
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 25 January 2021, pp. 2560-2587
- Print publication:
- December 2020
-
- Article
- Export citation
Erratum: Limiting properties of the distribution of primes in an arbitrarily large number of residue classes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 05 November 2020, pp. 1041-1044
- Print publication:
- December 2021
-
- Article
-
- You have access
- Export citation
Densities in certain three-way prime number races
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 12 October 2020, pp. 232-265
- Print publication:
- February 2022
-
- Article
- Export citation
Uniform convergence rate for Birkhoff means of certain uniquely ergodic toral maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 06 October 2020, pp. 3363-3388
- Print publication:
- November 2021
-
- Article
- Export citation
Some complexity results in the theory of normal numbers
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 28 September 2020, pp. 170-198
- Print publication:
- February 2022
-
- Article
- Export citation
Smale endomorphisms over graph-directed Markov systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 08 June 2020, pp. 2508-2541
- Print publication:
- August 2021
-
- Article
- Export citation
Maximizing Bernoulli measures and dimension gaps for countable branched systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 26 May 2020, pp. 1921-1939
- Print publication:
- July 2021
-
- Article
- Export citation
ON THE LONGEST BLOCK FUNCTION IN CONTINUED FRACTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 13 February 2020, pp. 196-206
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
Limiting Properties of the Distribution of Primes in an Arbitrarily Large Number of Residue Classes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 30 January 2020, pp. 837-849
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
MOMENTS OF RANDOM MULTIPLICATIVE FUNCTIONS, I: LOW MOMENTS, BETTER THAN SQUAREROOT CANCELLATION, AND CRITICAL MULTIPLICATIVE CHAOS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 20 January 2020, e1
-
- Article
-
- You have access
- Open access
- Export citation
SIMULTANEOUS DYNAMICAL DIOPHANTINE APPROXIMATION IN BETA EXPANSIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 186-195
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
Hausdorff dimension of divergent trajectories on homogeneous spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 2 / February 2020
- Published online by Cambridge University Press:
- 19 December 2019, pp. 340-359
- Print publication:
- February 2020
-
- Article
- Export citation
Equidistribution of Farey sequences on horospheres in covers of
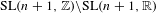 $\text{SL}(n+1,\mathbb{Z})\backslash \text{SL}(n+1,\mathbb{R})$ and applications
$\text{SL}(n+1,\mathbb{Z})\backslash \text{SL}(n+1,\mathbb{R})$ and applications
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 07 October 2019, pp. 471-493
- Print publication:
- February 2021
-
- Article
- Export citation
Optimal lower bounds for multiple recurrence
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 07 October 2019, pp. 379-407
- Print publication:
- February 2021
-
- Article
- Export citation
Continued fractions, the Chen–Stein method and extreme value theory
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 06 September 2019, pp. 461-470
- Print publication:
- February 2021
-
- Article
- Export citation
Generic point equivalence and Pisot numbers
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 11 July 2019, pp. 3169-3180
- Print publication:
- December 2020
-
- Article
- Export citation
Fast and slow points of Birkhoff sums
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 11 July 2019, pp. 3236-3256
- Print publication:
- December 2020
-
- Article
- Export citation
The sets of Dirichlet non-improvable numbers versus well-approximable numbers
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 27 June 2019, pp. 3217-3235
- Print publication:
- December 2020
-
- Article
- Export citation
A NOTE ON MATRIX APPROXIMATION IN THE THEORY OF MULTIPLICATIVE DIOPHANTINE APPROXIMATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 28 March 2019, pp. 372-377
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation