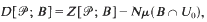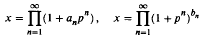Refine listing
Actions for selected content:
183 results in 11Kxx
Multiplicities of Higher Lie Characters
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 1 / August 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 9-21
- Print publication:
- August 2003
-
- Article
-
- You have access
- Export citation
Engel Series Expansions of Laurent Series and Hausdorff Dimensions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 1 / August 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-7
- Print publication:
- August 2003
-
- Article
-
- You have access
- Export citation
Density approximation and exact simulation of random variables that are solutions of fixed-point equations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 34 / Issue 2 / June 2002
- Published online by Cambridge University Press:
- 01 July 2016, pp. 441-468
- Print publication:
- June 2002
-
- Article
- Export citation
On the divisor function d(n): II
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 2 / December 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 419-423
- Print publication:
- December 1999
-
- Article
- Export citation
Notes on Erdös-Turán inequality
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 1 / August 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 51-57
- Print publication:
- August 1999
-
- Article
-
- You have access
- Export citation
β-transformation, invariant measure and uniform distribution
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 3 / June 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 418-428
- Print publication:
- June 1999
-
- Article
-
- You have access
- Export citation
The exact order of generalized diaphony and multidimensional numerical integration
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 1 / February 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-17
- Print publication:
- February 1999
-
- Article
-
- You have access
- Export citation
Non-expansive derived horseshoes
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 3 / December 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 405-415
- Print publication:
- December 1998
-
- Article
-
- You have access
- Export citation
On discrepancy bounds via dual shatter function
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 1 / June 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 42-49
- Print publication:
- June 1997
-
- Article
- Export citation
On the divisor function d(n)
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 2 / December 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 320-322
- Print publication:
- December 1996
-
- Article
- Export citation
Irregularities of distributions with respect to polytopes
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 1 / June 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 108-119
- Print publication:
- June 1996
-
- Article
- Export citation
On irregularities of distribution III
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 2 / April 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 228-244
- Print publication:
- April 1996
-
- Article
-
- You have access
- Export citation
Measures of sets decomposing the simply normal numbers in the unit interval
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 1 / June 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 164-172
- Print publication:
- June 1994
-
- Article
- Export citation
Irregularities of point distribution relative to convex polygons II
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 1 / June 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 127-136
- Print publication:
- June 1993
-
- Article
- Export citation
Irregularities of point distribution relative to half-planes I
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 1 / June 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 102-126
- Print publication:
- June 1993
-
- Article
- Export citation
Metrical properties of best approximants
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 53 / Issue 1 / August 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 78-91
- Print publication:
- August 1992
-
- Article
-
- You have access
- Export citation
Optimal approximation by continued fractions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 3 / June 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 481-504
- Print publication:
- June 1991
-
- Article
-
- You have access
- Export citation
Slice discrepancy and irregularities of distribution on spheres
- Part of
-
- Journal:
- Mathematika / Volume 38 / Issue 1 / June 1991
- Published online by Cambridge University Press:
- 26 February 2010, pp. 105-116
- Print publication:
- June 1991
-
- Article
- Export citation
Normality of some p—adic product expansions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 2 / October 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 258-263
- Print publication:
- October 1990
-
- Article
-
- You have access
- Export citation
Notes on uniform distribution modulo one
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 2 / October 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 264-272
- Print publication:
- October 1990
-
- Article
-
- You have access
- Export citation
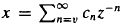 in an inderminate
in an inderminate 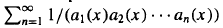 be the Engel expansin of Laurent series of
be the Engel expansin of Laurent series of 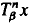 } are uniformly distributed. Here we consider the non-integer case, determine when
} are uniformly distributed. Here we consider the non-integer case, determine when 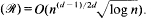 We prove that for
We prove that for 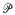 is a distribution of
is a distribution of 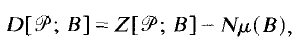
 is a distribution of
is a distribution of