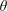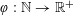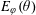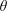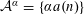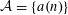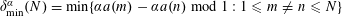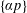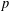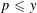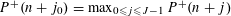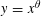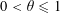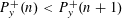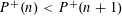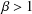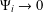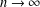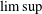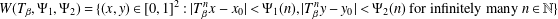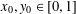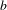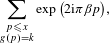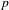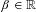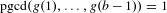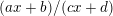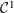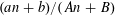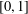Refine listing
Actions for selected content:
190 results in 11Kxx
HAUSDORFF DIMENSION OF THE SET APPROXIMATED BY IRRATIONAL ROTATIONS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 14 February 2018, pp. 267-283
- Print publication:
- 2018
-
- Article
- Export citation
HAUSDORFF MEASURE OF SETS OF DIRICHLET NON-IMPROVABLE NUMBERS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 19 April 2018, pp. 502-518
- Print publication:
- 2018
-
- Article
- Export citation
A METRIC THEORY OF MINIMAL GAPS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 3 / 2018
- Published online by Cambridge University Press:
- 21 May 2018, pp. 628-636
- Print publication:
- 2018
-
- Article
- Export citation
WEAK ADMISSIBILITY, PRIMITIVITY, O-MINIMALITY, AND DIOPHANTINE APPROXIMATION
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 17 April 2018, pp. 475-496
- Print publication:
- 2018
-
- Article
- Export citation
THE PRIMES ARE NOT METRIC POISSONIAN
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 14 February 2018, pp. 230-236
- Print publication:
- 2018
-
- Article
- Export citation
SUR LES PLUS GRANDS FACTEURS PREMIERSD’ENTIERS CONSÉCUTIFS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 05 April 2018, pp. 343-379
- Print publication:
- 2018
-
- Article
- Export citation
TWO-DIMENSIONAL SHRINKING TARGET PROBLEM IN BETA-DYNAMICAL SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 02 November 2017, pp. 33-42
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
PROPRIÉTÉS LOCALES DES CHIFFRES DES NOMBRES PREMIERS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 04 April 2017, pp. 189-224
- Print publication:
- January 2019
-
- Article
- Export citation
Non-trivial matrix actions preserve normality for continued fractions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 2 / February 2017
- Published online by Cambridge University Press:
- 06 February 2017, pp. 274-293
- Print publication:
- February 2017
-
- Article
- Export citation
POINT DISTRIBUTIONS IN COMPACT METRIC SPACES
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 1152-1171
- Print publication:
- 2017
-
- Article
- Export citation
A NOTE ON BADLY APPROXIMABLE LINEAR FORMS ON MANIFOLDS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 11 May 2017, pp. 587-601
- Print publication:
- 2017
-
- Article
-
- You have access
- HTML
- Export citation
TIGHTER BOUNDS FOR THE DISCREPANCY OF BOXESAND POLYTOPES
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 1091-1113
- Print publication:
- 2017
-
- Article
- Export citation
DISCREPANCY OF SECOND ORDER DIGITAL SEQUENCES IN FUNCTION SPACES WITH DOMINATING MIXED SMOOTHNESS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 863-894
- Print publication:
- 2017
-
- Article
- Export citation
HARMONIC ANALYSIS ON THE POSITIVE RATIONALS. DETERMINATION OF THE GROUP GENERATED BY THE RATIOS
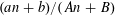 $(an+b)/(An+B)$
$(an+b)/(An+B)$
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 919-943
- Print publication:
- 2017
-
- Article
- Export citation
A New Quasi-Monte Carlo Technique Based on Nonnegative Least Squares and Approximate Fekete Points
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 9 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 17 November 2016, pp. 640-663
- Print publication:
- November 2016
-
- Article
- Export citation
DYNAMICS ON SUPERSINGULAR K3 SURFACES AND AUTOMORPHISMS OF SALEM DEGREE 22
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 227 / September 2017
- Published online by Cambridge University Press:
- 13 October 2016, pp. 1-15
-
- Article
-
- You have access
- HTML
- Export citation
ON POINTS WITH POSITIVE DENSITY OF THE DIGIT SEQUENCE IN INFINITE ITERATED FUNCTION SYSTEMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 09 September 2016, pp. 435-443
-
- Article
-
- You have access
- Export citation
RESTRICTED SIMULTANEOUS DIOPHANTINE APPROXIMATION
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 26 July 2016, pp. 34-52
- Print publication:
- 2017
-
- Article
- Export citation
Sur les processus arithmétiques liés aux diviseurs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue A / July 2016
- Published online by Cambridge University Press:
- 25 July 2016, pp. 63-76
- Print publication:
- July 2016
-
- Article
- Export citation
A NOTE ON WEIGHTED BADLY APPROXIMABLE LINEAR FORMS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 349-357
-
- Article
-
- You have access
- Export citation