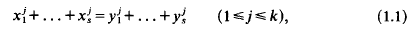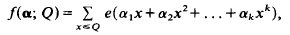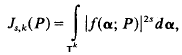Refine listing
Actions for selected content:
214 results in 11Pxx
The values of ternary quadratic forms at prime arguments
- Part of
-
- Journal:
- Mathematika / Volume 51 / Issue 1-2 / December 2004
- Published online by Cambridge University Press:
- 26 February 2010, pp. 83-96
- Print publication:
- December 2004
-
- Article
- Export citation
The arithmetic of partitions into distinct parts
- Part of
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 203-211
- Print publication:
- December 2001
-
- Article
- Export citation
The inverse Goldbach problem
- Part of
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 151-158
- Print publication:
- December 2001
-
- Article
- Export citation
Sums of three cubes
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 53-61
- Print publication:
- December 2000
-
- Article
- Export citation
Additive representation in thin sequences, II: The binary Goldbach problem
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 117-125
- Print publication:
- December 2000
-
- Article
- Export citation
Non-vanishing of the partition function modulo odd primes l
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 185-192
- Print publication:
- June 1999
-
- Article
- Export citation
Sums of k-th powers in number fields
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 2 / December 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 359-370
- Print publication:
- December 1998
-
- Article
- Export citation
On gaps between numbers that are sums of three cubes
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 1 / June 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-13
- Print publication:
- June 1997
-
- Article
- Export citation
On the sum of four cubes
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 2 / December 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 323-348
- Print publication:
- December 1996
-
- Article
- Export citation
A pair correlation hypothesis and the exceptional set in Goldbach's problem
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 2 / December 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 349-361
- Print publication:
- December 1996
-
- Article
- Export citation
The asymptotic formula in Waring's problem
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 2 / December 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 329-347
- Print publication:
- December 1994
-
- Article
- Export citation
On the exceptional set for the sum of a prime and a k-th power
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 400-421
- Print publication:
- December 1992
-
- Article
- Export citation
Linear equations in primes
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 367-378
- Print publication:
- December 1992
-
- Article
- Export citation
On Vinogradov's mean value theorem
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 379-399
- Print publication:
- December 1992
-
- Article
- Export citation
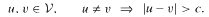
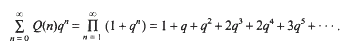
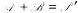 where, ℝ′ differs from the set of primes in finitely many elements only and
where, ℝ′ differs from the set of primes in finitely many elements only and 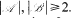 .
.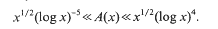
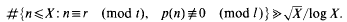
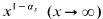 with
with 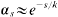 for large
for large 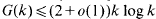 for large
for large 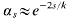 .
.
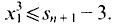 Then
Then 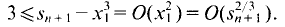 This procedure is iterated by choosing
This procedure is iterated by choosing 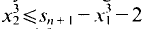 and
and 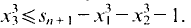 Thus
Thus 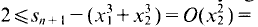
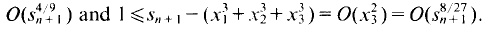 Since
Since 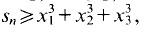 this implies (1).
this implies (1).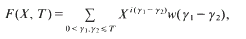
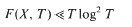
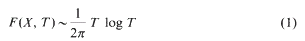

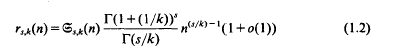
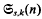 , the
, the 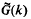 to be the smallest value of
to be the smallest value of