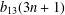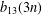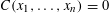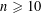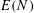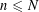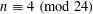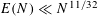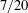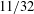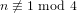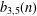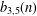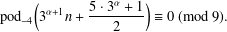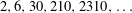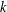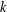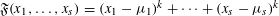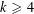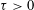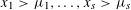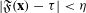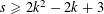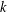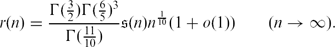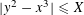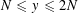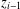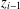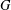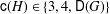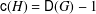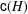Refine listing
Actions for selected content:
211 results in 11Pxx
REFINEMENTS OF THE FIRST AND SECOND POSITIVE CRANK MOMENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 17 February 2016, pp. 236-244
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
THE 7-REGULAR AND 13-REGULAR PARTITION FUNCTIONS MODULO 3
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 11 January 2016, pp. 410-419
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
RATIONAL POINTS ON CUBIC HYPERSURFACES THAT SPLIT INTO FOUR FORMS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 29 January 2016, pp. 430-440
- Print publication:
- 2016
-
- Article
- Export citation
ON SUMS OF FOUR SQUARES OF PRIMES
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 22 January 2016, pp. 348-361
- Print publication:
- 2016
-
- Article
- Export citation
WARING’S PROBLEM WITH PIATETSKI-SHAPIRO NUMBERS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 17 February 2016, pp. 524-550
- Print publication:
- 2016
-
- Article
- Export citation
A GENERALIZATION OF THE DISCRETE VERSION OF MINKOWSKI’S FUNDAMENTAL THEOREM
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 29 February 2016, pp. 637-652
- Print publication:
- 2016
-
- Article
- Export citation
EXPONENTIAL SUMS OVER PRIMES IN SHORT INTERVALS AND AN APPLICATION TO THE WARING–GOLDBACH PROBLEM
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 17 February 2016, pp. 508-523
- Print publication:
- 2016
-
- Article
- Export citation
On the sum of the square of a prime and a square-free number
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 January 2016, pp. 16-24
-
- Article
-
- You have access
- Export citation
CONGRUENCES MODULO 2 FOR CERTAIN PARTITION FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 11 November 2015, pp. 400-409
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
On n-Sums in an Abelian Group
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 3 / May 2016
- Published online by Cambridge University Press:
- 03 November 2015, pp. 419-435
-
- Article
- Export citation
A REMARK ON TAIL DISTRIBUTIONS OF PARTITION RANK AND CRANK
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 20 August 2015, pp. 31-36
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
ARITHMETIC PROPERTIES OF PARTITION QUADRUPLES WITH ODD PARTS DISTINCT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 08 July 2015, pp. 353-364
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Rational points on linear slices of diagonal hypersurfaces
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 218 / June 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 51-100
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
THE JUMPING CHAMPION CONJECTURE
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 04 May 2015, pp. 719-740
- Print publication:
- September 2015
-
- Article
- Export citation
WARING’S PROBLEM WITH SHIFTS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 06 March 2015, pp. 13-46
- Print publication:
- 2016
-
- Article
- Export citation
The Sharp Threshold for Maximum-Size Sum-Free Subsets in Even-Order Abelian Groups
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 4 / July 2015
- Published online by Cambridge University Press:
- 09 January 2015, pp. 609-640
-
- Article
- Export citation
ON THE ASYMPTOTIC FORMULA IN WARING'S PROBLEM: ONE SQUARE AND THREE FIFTH POWERS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 18 December 2014, pp. 681-692
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
THE NUMBER OF SOLUTIONS TO MORDELL’S EQUATION IN CONSTRAINED RANGES
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 05 December 2014, pp. 708-718
- Print publication:
- September 2015
-
- Article
- Export citation
THE CATENARY DEGREE OF KRULL MONOIDS II
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 21 November 2014, pp. 324-354
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
FURTHER RESULTS ON VANISHING COEFFICIENTS IN INFINITE PRODUCT EXPANSIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 11 November 2014, pp. 69-77
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation