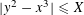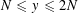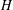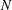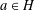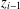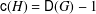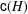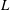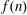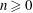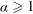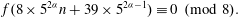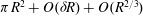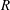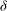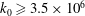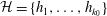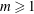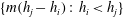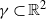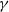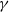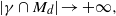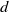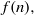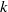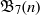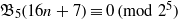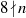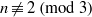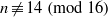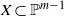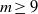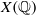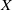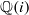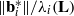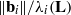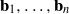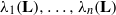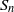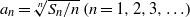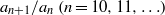Refine listing
Actions for selected content:
214 results in 11Pxx
THE NUMBER OF SOLUTIONS TO MORDELL’S EQUATION IN CONSTRAINED RANGES
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 05 December 2014, pp. 708-718
- Print publication:
- September 2015
-
- Article
- Export citation
THE CATENARY DEGREE OF KRULL MONOIDS II
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 21 November 2014, pp. 324-354
-
- Article
-
- You have access
- Export citation
FURTHER RESULTS ON VANISHING COEFFICIENTS IN INFINITE PRODUCT EXPANSIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 11 November 2014, pp. 69-77
-
- Article
-
- You have access
- Export citation
AN
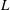 $L$ -FUNCTION-FREE PROOF OF VINOGRADOV’S THREE PRIMES THEOREM
$L$ -FUNCTION-FREE PROOF OF VINOGRADOV’S THREE PRIMES THEOREM
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 04 November 2014, e27
-
- Article
-
- You have access
- Open access
- Export citation
ON IMPROVING ROTH’S THEOREM IN THE PRIMES
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 09 October 2014, pp. 49-62
- Print publication:
- January 2015
-
- Article
- Export citation
A NEW CONGRUENCE MODULO 25 FOR 1-SHELL TOTALLY SYMMETRIC PLANE PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 08 October 2014, pp. 41-46
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
INFINITE FAMILIES OF CONGRUENCES MODULO 3 AND 9 FOR BIPARTITIONS WITH 3-CORES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 27 August 2014, pp. 47-52
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
RATIONAL POINTS ON INTERSECTIONS OF CUBIC AND QUADRIC HYPERSURFACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 4 / October 2015
- Published online by Cambridge University Press:
- 05 June 2014, pp. 703-749
- Print publication:
- October 2015
-
- Article
- Export citation
GENERALISATION OF KEITH’S CONJECTURE ON 9-REGULAR PARTITIONS AND 3-CORES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 20 May 2014, pp. 204-212
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
NEW INFINITE FAMILIES OF CONGRUENCES MODULO 4 AND 8 FOR 1-SHELL TOTALLY SYMMETRIC PLANE PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 02 April 2014, pp. 37-46
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
THE TILED CIRCLE PROBLEM
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 2 / July 2014
- Published online by Cambridge University Press:
- 31 March 2014, pp. 321-346
- Print publication:
- July 2014
-
- Article
- Export citation
A NOTE ON THE POLIGNAC NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 13 March 2014, pp. 500-502
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
CONVEX CURVES AND A POISSON IMITATION OF LATTICES
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 02 January 2014, pp. 139-152
- Print publication:
- January 2014
-
- Article
- Export citation
ARITHMETIC PROPERTIES OF 1-SHELL TOTALLY SYMMETRIC PLANE PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 27 September 2013, pp. 473-478
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
CONGRUENCES MODULO POWERS OF 2 FOR FU’S 5 DOTS BRACELET PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 22 August 2013, pp. 360-372
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
ON WARING’S PROBLEM: TWO SQUARES AND THREE BIQUADRATES
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 28 June 2013, pp. 153-165
- Print publication:
- January 2014
-
- Article
- Export citation
Rational points on singular intersections of quadrics
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 9 / September 2013
- Published online by Cambridge University Press:
- 20 June 2013, pp. 1457-1494
- Print publication:
- September 2013
-
- Article
- Export citation
SLIDE REDUCTION, SUCCESSIVE MINIMA AND SEVERAL APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 30 April 2013, pp. 390-406
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
ON A SEQUENCE INVOLVING SUMS OF PRIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 18 January 2013, pp. 197-205
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
Efficient implementation of the Hardy–Ramanujan–Rademacher formula
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 October 2012, pp. 341-359
-
- Article
-
- You have access
- Export citation