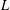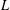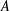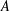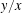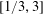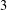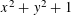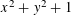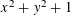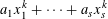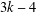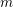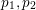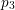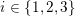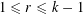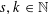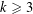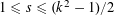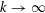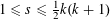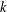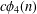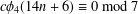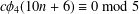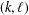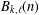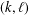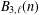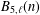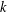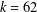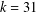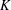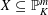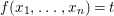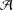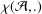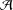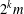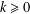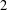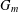Refine listing
Actions for selected content:
211 results in 11Pxx
GOLDBACH REPRESENTATIONS IN ARITHMETIC PROGRESSIONS AND ZEROS OF DIRICHLET L-FUNCTIONS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 1 / 2019
- Published online by Cambridge University Press:
- 24 August 2018, pp. 57-97
- Print publication:
- 2019
-
- Article
- Export citation
Limit Shapes via Bijections
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 2 / March 2019
- Published online by Cambridge University Press:
- 02 August 2018, pp. 187-240
-
- Article
- Export citation
FINITELY STABLE ADDITIVE BASES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 20 February 2018, pp. 360-362
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
TRIANGLES CAPTURING MANY LATTICE POINTS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 25 April 2018, pp. 551-582
- Print publication:
- 2018
-
- Article
- Export citation
WEAK ADMISSIBILITY, PRIMITIVITY, O-MINIMALITY, AND DIOPHANTINE APPROXIMATION
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 17 April 2018, pp. 475-496
- Print publication:
- 2018
-
- Article
- Export citation
THE GOLDBACH PROBLEM FOR PRIMES THAT ARE SUMS OF TWO SQUARES PLUS ONE
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 25 January 2018, pp. 20-70
- Print publication:
- 2018
-
- Article
- Export citation
THE DENSITY OF NUMBERS REPRESENTED BY DIAGONAL FORMS OF LARGE DEGREE
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 23 April 2018, pp. 542-550
- Print publication:
- 2018
-
- Article
- Export citation
THE
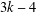 $3k-4$ THEOREM FOR ORDERED GROUPS
$3k-4$ THEOREM FOR ORDERED GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 28 September 2017, pp. 43-46
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
Vinogradov’s three primes theorem with almost twin primes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 6 / June 2017
- Published online by Cambridge University Press:
- 20 April 2017, pp. 1220-1256
- Print publication:
- June 2017
-
- Article
- Export citation
RATIONAL POINTS ON THE INNER PRODUCT CONE VIA THE HYPERBOLA METHOD
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 780-796
- Print publication:
- 2017
-
- Article
- Export citation
VINOGRADOV SYSTEMS WITH A SLICE OFF
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 797-817
- Print publication:
- 2017
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
APPROXIMATING THE MAIN CONJECTURE IN VINOGRADOV’S MEAN VALUE THEOREM
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 21 December 2016, pp. 292-350
- Print publication:
- 2017
-
- Article
- Export citation
CONGRUENCES MODULO 5 AND 7 FOR 4-COLORED GENERALIZED FROBENIUS PARTITIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 21 December 2016, pp. 157-176
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
ARITHMETIC PROPERTIES OF
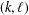 $(k,\ell )$ -REGULAR BIPARTITIONS
$(k,\ell )$ -REGULAR BIPARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 01 December 2016, pp. 353-364
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
ON PAIRS OF GOLDBACH–LINNIK EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 19 October 2016, pp. 199-208
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
FORMS OF DIFFERING DEGREES OVER NUMBER FIELDS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 26 September 2016, pp. 92-123
- Print publication:
- 2017
-
- Article
- Export citation
On the Chromatic Number of Random Cayley Graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 2 / March 2017
- Published online by Cambridge University Press:
- 09 September 2016, pp. 248-266
-
- Article
- Export citation
THE QUADRATIC FORM IN NINE PRIME VARIABLES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 223 / Issue 1 / September 2016
- Published online by Cambridge University Press:
- 18 August 2016, pp. 21-65
- Print publication:
- September 2016
-
- Article
-
- You have access
- HTML
- Export citation
ALMOST ALL PRIMES HAVE A MULTIPLE OF SMALL HAMMING WEIGHT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 23 May 2016, pp. 224-235
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
SETS WITH EVEN PARTITION FUNCTIONS AND CYCLOTOMIC NUMBERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 14 March 2016, pp. 289-302
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation