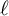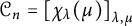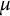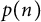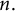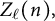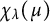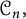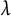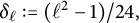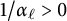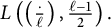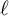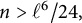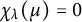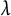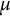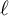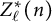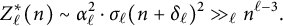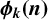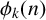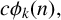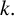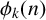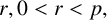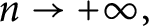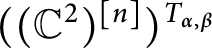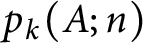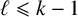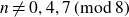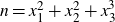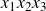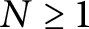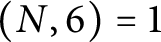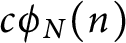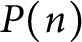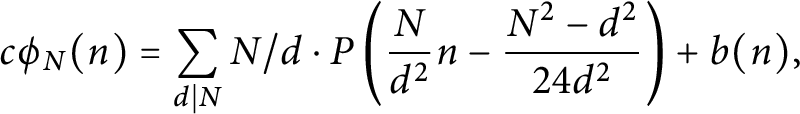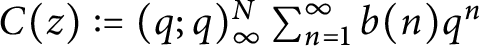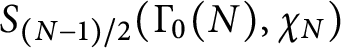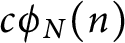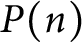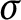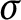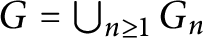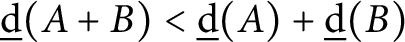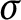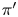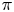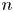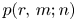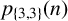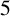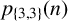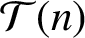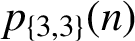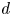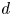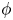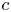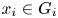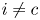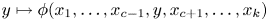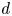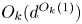Refine listing
Actions for selected content:
211 results in 11Pxx
Distributions on partitions arising from Hilbert schemes and hook lengths
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 29 June 2022, e49
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Zeros in the character tables of symmetric groups with an
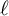 $\ell $-core index
$\ell $-core index
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 27 June 2022, pp. 467-476
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE PARITY OF THE GENERALISED FROBENIUS PARTITION FUNCTIONS
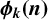 $\boldsymbol {\phi _k(n)}$
$\boldsymbol {\phi _k(n)}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 15 June 2022, pp. 431-436
- Print publication:
- December 2022
-
- Article
- Export citation
Limiting Betti distributions of Hilbert schemes on n points
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 13 May 2022, pp. 243-258
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bounds for spectral projectors on tori
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 12 May 2022, e24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE INHOMOGENEOUS VINOGRADOV SYSTEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 19 April 2022, pp. 396-403
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Uniform bounds for norms of theta series and arithmetic applications
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 28 February 2022, pp. 669-691
- Print publication:
- November 2022
-
- Article
- Export citation
AN EXPLICIT VERSION OF CHEN’S THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 344-346
- Print publication:
- April 2022
-
- Article
-
- You have access
- HTML
- Export citation
N-colored generalized Frobenius partitions: generalized Kolitsch identities
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 25 January 2022, pp. 447-469
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Kneser’s theorem in
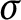 $\sigma $-finite abelian groups
$\sigma $-finite abelian groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 10 January 2022, pp. 936-942
- Print publication:
- December 2022
-
- Article
- Export citation
Some generating functions and inequalities for the andrews–stanley partition functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 27 December 2021, pp. 120-135
-
- Article
- Export citation
PROOF OF SOME CONJECTURAL CONGRUENCES OF DA SILVA AND SELLERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 13 December 2021, pp. 57-61
- Print publication:
- August 2022
-
- Article
- Export citation
SZEMERÉDI’S THEOREM: AN EXPLORATION OF IMPURITY, EXPLANATION, AND CONTENT
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 03 December 2021, pp. 700-739
- Print publication:
- September 2023
-
- Article
- Export citation
TIGHT UNIVERSAL TRIANGULAR FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 18 November 2021, pp. 372-384
- Print publication:
- June 2022
-
- Article
- Export citation
ON WARING’S PROBLEM IN SUMS OF THREE CUBES FOR SMALLER POWERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 16 September 2021, pp. 378-405
- Print publication:
- June 2023
-
- Article
- Export citation
A PROOF OF MERCA’S CONJECTURES ON SUMS OF ODD DIVISOR FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 10 September 2021, pp. 197-201
- Print publication:
- April 2022
-
- Article
- Export citation
ARITHMETIC PROPERTIES OF 3-REGULAR PARTITIONS IN THREE COLOURS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 07 June 2021, pp. 415-423
- Print publication:
- December 2021
-
- Article
- Export citation
On the distribution of the digits of quotients of integers and primes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 279-295
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on extensions of multilinear maps defined on multilinear varieties
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 148-173
-
- Article
- Export citation
Additive bases via Fourier analysis
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 29 April 2021, pp. 930-941
-
- Article
- Export citation