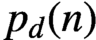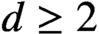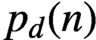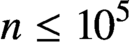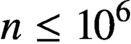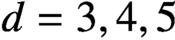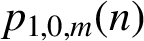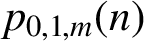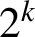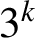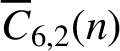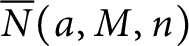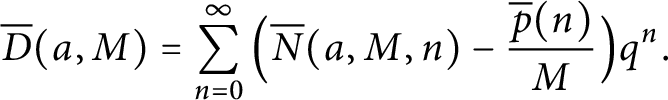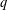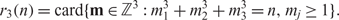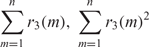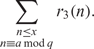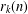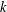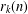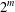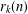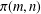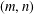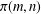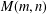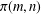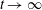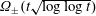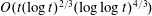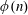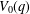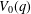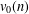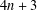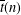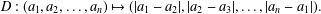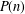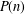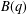Refine listing
Actions for selected content:
210 results in 11Pxx
SOME OBSERVATIONS AND SPECULATIONS ON PARTITIONS INTO d-TH POWERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 28 January 2021, pp. 406-414
- Print publication:
- December 2021
-
- Article
-
- You have access
- Open access
- Export citation
BIASES IN INTEGER PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 14 January 2021, pp. 177-186
- Print publication:
- October 2021
-
- Article
- Export citation
DIVISIBILITY OF CERTAIN SINGULAR OVERPARTITIONS BY POWERS OF
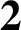 $\textbf{2}$ AND
$\textbf{2}$ AND 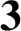 $\textbf{3}$
$\textbf{3}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 14 January 2021, pp. 238-248
- Print publication:
- October 2021
-
- Article
- Export citation
ON THE SUM OF PARTS IN THE PARTITIONS OF n INTO DISTINCT PARTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 11 December 2020, pp. 228-237
- Print publication:
- October 2021
-
- Article
- Export citation
DISTRIBUTION OF INTEGERS WITH PRESCRIBED STRUCTURE AND APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 19 October 2020, pp. 509-511
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
Newman's identities, lucas sequences and congruences for certain partition functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 3 / August 2020
- Published online by Cambridge University Press:
- 08 October 2020, pp. 709-736
-
- Article
- Export citation
THE ROGERS–RAMANUJAN CONTINUED FRACTION AND RELATED ETA-QUOTIENT REPRESENTATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 17 September 2020, pp. 248-259
- Print publication:
- April 2021
-
- Article
- Export citation
Dyson’s rank, overpartitions, and universal mock theta functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 07 September 2020, pp. 687-696
- Print publication:
- September 2021
-
- Article
- Export citation
SUMS OF PARTIAL THETA FUNCTIONS THROUGH AN EXTENDED BAILEY TRANSFORM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 13 May 2020, pp. 1-10
- Print publication:
- February 2021
-
- Article
- Export citation
ON SOME QUESTIONS OF PARTITIO NUMERORUM: TRES CUBI
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 21 April 2020, pp. 223-244
- Print publication:
- January 2021
-
- Article
- Export citation
SUMS OF SQUARES AND PARTITION CONGRUENCES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 18 March 2020, pp. 249-267
- Print publication:
- October 2021
-
- Article
- Export citation
POWER PARTITIONS AND SEMI-
 $m$-FIBONACCI PARTITIONS
$m$-FIBONACCI PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 20 February 2020, pp. 418-429
- Print publication:
- December 2020
-
- Article
- Export citation
UNIFORM ASYMPTOTIC FORMULAS FOR RESTRICTED BIPARTITE PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 05 February 2020, pp. 217-225
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
Primitive Points in Rational Polygons
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 30 January 2020, pp. 850-870
- Print publication:
- December 2020
-
- Article
- Export citation
OVERPARTITIONS RELATED TO THE MOCK THETA FUNCTION
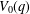 $V_{0}(q)$
$V_{0}(q)$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 16 January 2020, pp. 410-417
- Print publication:
- December 2020
-
- Article
- Export citation
INFINITE FAMILIES OF CONGRUENCES FOR OVERPARTITIONS WITH RESTRICTED ODD DIFFERENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 59-66
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
ON SUMS OF TWO PRIME SQUARES, FOUR PRIME CUBES AND POWERS OF TWO
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 207-216
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
LOWER BOUNDS FOR PERIODS OF DUCCI SEQUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 22 November 2019, pp. 31-38
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
ARITHMETIC PROPERTIES OF COEFFICIENTS OF THE MOCK THETA FUNCTION
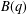 $B(q)$
$B(q)$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 21 November 2019, pp. 50-58
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Vinogradov’s three primes theorem with primes having given primitive roots
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 05 November 2019, pp. 75-110
- Print publication:
- January 2021
-
- Article
- Export citation