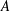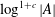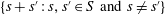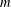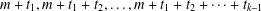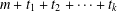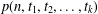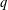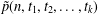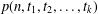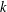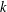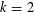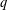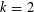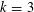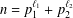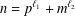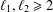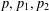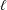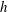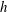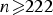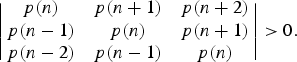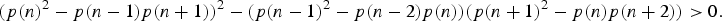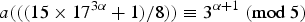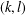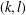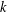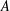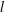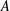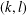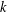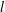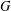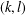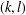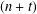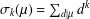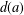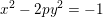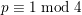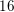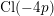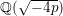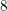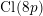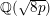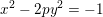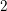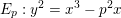Refine listing
Actions for selected content:
211 results in 11Pxx
Vinogradov’s three primes theorem with primes having given primitive roots
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 05 November 2019, pp. 75-110
- Print publication:
- January 2021
-
- Article
- Export citation
Polylogarithmic bounds in the nilpotent Freiman theorem
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 08 October 2019, pp. 111-127
- Print publication:
- January 2021
-
- Article
- Export citation
The Erdős–Moser Sum-free Set Problem
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 23 September 2019, pp. 63-107
- Print publication:
- February 2021
-
- Article
- Export citation
GENERALISATION OF A RESULT ON DISTINCT PARTITIONS WITH BOUNDED PART DIFFERENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 24 July 2019, pp. 233-237
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
PARTITIONS WITH AN ARBITRARY NUMBER OF SPECIFIED DISTANCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 03 June 2019, pp. 35-39
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
A PROOF OF ANDREWS’ CONJECTURE ON PARTITIONS WITH NO SHORT SEQUENCES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 30 May 2019, e17
-
- Article
-
- You have access
- Open access
- Export citation
SHORT INTERVALS ASYMPTOTIC FORMULAE FOR BINARY PROBLEMS WITH PRIME POWERS, II
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 08 April 2019, pp. 351-370
- Print publication:
- December 2020
-
- Article
- Export citation
ON THE DISTRIBUTION OF THE RANK STATISTIC FOR STRONGLY CONCAVE COMPOSITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 13 February 2019, pp. 230-238
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
Zeroes of Polynomials With Prime Inputs and Schmidt’s
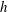 $h$-invariant
$h$-invariant
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 07 February 2019, pp. 805-833
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Determinantal inequalities for the partition function
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 1451-1466
- Print publication:
- June 2020
-
- Article
- Export citation
Infinite families of congruences modulo 5 and 7 for the cubic partition function
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1189-1205
- Print publication:
- October 2019
-
- Article
- Export citation
ON ITERATED PRODUCT SETS WITH SHIFTS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 4 / 2019
- Published online by Cambridge University Press:
- 21 May 2019, pp. 831-850
- Print publication:
- 2019
-
- Article
- Export citation
A problem of integer partitions and numerical semigroups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 969-978
- Print publication:
- August 2019
-
- Article
- Export citation
THE MAXIMUM SIZE OF
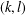 $(k,l)$-SUM-FREE SETS IN CYCLIC GROUPS
$(k,l)$-SUM-FREE SETS IN CYCLIC GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 26 December 2018, pp. 184-194
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
AN ANALOGUE OF EULER’S IDENTITY AND SPLIT PERFECT PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 17 December 2018, pp. 353-361
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Spins of prime ideals and the negative Pell equation
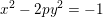 $x^{2}-2py^{2}=-1$
$x^{2}-2py^{2}=-1$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 23 November 2018, pp. 100-125
- Print publication:
- January 2019
-
- Article
- Export citation
PARITY RESULTS FOR PARTITIONS WHEREIN EACH PART APPEARS AN ODD NUMBER OF TIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 12 November 2018, pp. 51-55
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
PRIME SOLUTIONS TO POLYNOMIAL EQUATIONS IN MANY VARIABLES AND DIFFERING DEGREES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 18 October 2018, e19
-
- Article
-
- You have access
- Open access
- Export citation
FOUR IDENTITIES FOR THIRD ORDER MOCK THETA FUNCTIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 239 / September 2020
- Published online by Cambridge University Press:
- 21 September 2018, pp. 173-204
- Print publication:
- September 2020
-
- Article
-
- You have access
- HTML
- Export citation
SARNAK’S SATURATION PROBLEM FOR COMPLETE INTERSECTIONS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 1 / 2019
- Published online by Cambridge University Press:
- 24 August 2018, pp. 1-56
- Print publication:
- 2019
-
- Article
- Export citation