We develop Weyl differencing and Hua-type lemmata for a class of multidimensional exponential sums. We then apply our estimates to bound the number of variables required to establish an asymptotic formula for the number of solutions of a system of diophantine equations arising from the study of linear spaces on hypersurfaces. For small values of the degree and dimension, our results are superior to those stemming from the author’s earlier work on Vinogradov’s mean value theorem.

In this paper, we consider the simultaneous representation of pairs of positive integers. We show that every pair of large positive even integers can be represented in the form of a pair of linear equations in four prime variables and k powers of two. Here, k=63 in general and k=31 under the generalised Riemann hypothesis.

We apply a method of Davenport to improve several estimates for slim exceptional sets associated with the asymptotic formula in Waring’s problem. In particular, we show that the anticipated asymptotic formula in Waring’s problem for sums of seven cubes holds for all but O(N1/3+ε) of the natural numbers not exceeding N.

We prove two results about the asymptotic formula for The first result is for x7/12+ε≤h≤x and h/(log x)B≤Q≤h, where ε,B>0 are arbitrary constants. For the second result we assume that the Generalized Riemann Hypothesis holds and we obtain a stronger error term and a better uniformity on h.

We study the variance of the fluctuations in the number of lattice points in a ball and in a thin spherical shell of large radius centred at a Diophantine point.

We extend Kemperman's structure theorem by completely characterizing those finite subsets A and B of an arbitrary abelian group with |A + B| = |A| + |B|.

Let R(n,θ) denote the number of representations of the natural number n as the sum of four squares, each composed only with primes not exceeding nθ/2. When θ>e−1/3 a lower bound for R(n,θ) of the expected order of magnitude is established, and when θ>365/592, it is shown that R(n,θ)>0 holds for large n. A similar result is obtained for sums of three squares. An asymptotic formula is obtained for the related problem of representing an integer as the sum of two squares and two squares composed of small primes, as above, for any fixed θ>0. This last result is the key to bound R(n,θ) from below.

In a recent paper, Calkin et al. [N. Calkin, N. Drake, K. James, S. Law, P. Lee, D. Penniston and J. Radder, ‘Divisibility properties of the 5-regular and 13-regular partition functions’, Integers8 (2008), #A60] used the theory of modular forms to examine 5-regular partitions modulo 2 and 13-regular partitions modulo 2 and 3; they obtained and conjectured various results. In this note, we use nothing more than Jacobi’s triple product identity to obtain results for 5-regular partitions that are stronger than those obtained by Calkin and his collaborators. We find infinitely many Ramanujan-type congruences for b5(n), and we prove the striking result that the number of 5-regular partitions of the number n is even for at least 75% of the positive integers n.

Using the framework of overpartitions, we give a combinatorial interpretation and proof of the q-Bailey identity. We then deduce from this identity a couple of facts about overpartitions. We show that the method of proof of the q-Bailey identity also applies to the (first) q-Gauss identity.

Using elementary means, we derive an explicit formula for a3(n), the number of 3-core partitions of n, in terms of the prime factorization of 3n+1. Based on this result, we are able to prove several infinite families of arithmetic results involving a3(n), one of which specializes to the recent result of Baruah and Berndt which states that, for all n≥0, a3(4n+1)=a3(n).

Suppose that G is an abelian group and that A ⊂ G is finite and contains no non-trivial three-term arithmetic progressions. We show that |A+A| »ε|A|(log|A|)⅓−ε.

Erdős and Odlyzko proved that odd integers k such that k2n+1 is prime for some positive integer n have a positive lower density. In this paper, we characterize all arithmetic progressions in which natural numbers that can be expressed in the form (p−1)2−n (where p is a prime number) have a positive proportion. We also prove that an arithmetic progression consisting of odd numbers can be obtained from a covering system if and only if those integers in such a progression which can be expressed in the form (p−1)2−n have an asymptotic density of zero.

An asymptotic estimate is obtained for the number of partitions of the positive integer n into unequal parts coming from a sequence u, with each part greater than m, under suitable conditions on the sequence u. The estimate holds uniformly with respect to integers m such that 0 ≤ m ≤ n1−δ, as n → ∞, where δ is a given real number, such that 0 < δ < 1.

In this article we study some special problems of the additive number theory connected with an estimate of cardinality of a sum of two sets, which can be convex as well as non-convex sequences.

For the purpose of this paper, we call a set of positive reals ν a well-spaced set if there is a c > 0 such that

An asymptotic formula is established for the number of representations of a large integer as the sum of kth powers of natural numbers, in which each representation is counted with a homogeneous weight that de-emphasises the large solutions. Such an asymptotic formula necessarily fails when this weight is excessively light.

A partition of the positive integer n into distinct parts is a decreasing sequence of positive integers whose sum is n, and the number of such partitions is denoted by Q(n). If we adopt the convention that Q(0) = 1, then we have the generating function

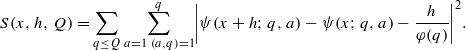
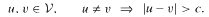
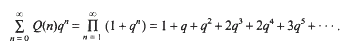
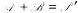Improved upper and lower bounds of the counting functions of the conceivable additive decomposition sets of the set of primes are established. Suppose that where, ℝ′ differs from the set of primes in finitely many elements only and .

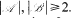It is shown that the counting functions A(x) of ℐ and B(x) of ℬ for sufficiently large x, satisfy

The set of integers represented as the sum of three cubes of natural numbers is widely expected to have positive density (see Hooley [7] for a discussion of this topic). Over the past six decades or so, the pursuit of an acceptable approximation to the latter statement has spawned much of the progress achieved in the theory of the Hardy-Littlewood method, so far as its application to Waring's problem for smaller exponents is concerned. Write R(N) for the number of positive integers not exceeding N which are the sum of three cubes of natural numbers.

§1. Introduction. Most prominent among the classical problems in additive number theory are those of Waring and Goldbach type. Although use of the Hardy–Littlewood method has brought admirable progress, the finer questions associated with such problems have yet to find satisfactory solutions. For example, while the ternary Goldbach problem was solved by Vinogradov as early as 1937 (see Vinogradov [16], [17]), the latter's methods permit one to establish merely that almost all even integers are the sum of two primes (see Chudakov [4], van der Corput [5] and Estermann [7]).