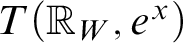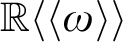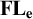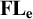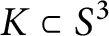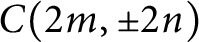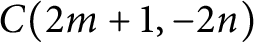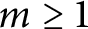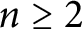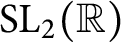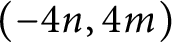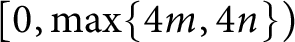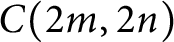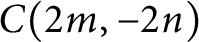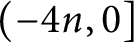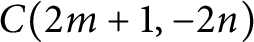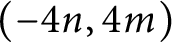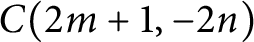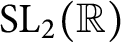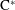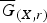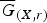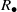Refine listing
Actions for selected content:
58 results in 06Fxx
The type semigroup, comparison, and almost finiteness for ample groupoids
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 27 October 2021, pp. 361-400
- Print publication:
- February 2023
-
- Article
- Export citation
MODAL OPERATORS ON RINGS OF CONTINUOUS FUNCTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 08 October 2021, pp. 1322-1348
- Print publication:
- December 2022
-
- Article
- Export citation
SURREAL ORDERED EXPONENTIAL FIELDS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 13 August 2021, pp. 1066-1115
- Print publication:
- September 2021
-
- Article
- Export citation
MOST SIMPLE EXTENSIONS OF
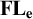 $\textbf{FL}_{\textbf{e}}$ ARE UNDECIDABLE
$\textbf{FL}_{\textbf{e}}$ ARE UNDECIDABLE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 10 June 2021, pp. 1156-1200
- Print publication:
- September 2022
-
- Article
- Export citation
Bi-orders do not arise from total orders
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 20 April 2021, pp. 217-224
- Print publication:
- March 2022
-
- Article
- Export citation
Left orderable surgeries of double twist knots II
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 27 August 2020, pp. 624-637
- Print publication:
- September 2021
-
- Article
- Export citation
Edwards' condition for quasitraces on C*-algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 08 April 2020, pp. 525-547
- Print publication:
- April 2021
-
- Article
-
- You have access
- Open access
- Export citation
Orders on Trees and Free Products of Left-ordered Groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 31 March 2020, pp. 335-347
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Dense Orderings in the Space of Left-orderings of a Group
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 17 December 2019, pp. 393-404
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Nearly Approximate Transitivity (AT) for Circulant Matrices
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 07 March 2019, pp. 381-415
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
On Structure Groups of Set-Theoretic Solutions to the Yang–Baxter Equation
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 11 January 2019, pp. 683-717
-
- Article
- Export citation
An Equivariant Theory for the Bivariant Cuntz Semigroup
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 04 April 2018, pp. 573-598
-
- Article
- Export citation
FINITE-DIMENSIONAL ORDERED VECTOR SPACES WITH RIESZ INTERPOLATION AND EFFROS–SHEN’S UNIMODULARITY CONJECTURE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 13 May 2016, pp. 277-287
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
SOLVABLE LIE GROUPS DEFINABLE IN O-MINIMAL THEORIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 28 April 2016, pp. 441-452
- Print publication:
- April 2018
-
- Article
- Export citation
CHARACTERIZATION OF PROJECTIVE QUANTALES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 08 January 2016, pp. 403-420
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
THE ZELEZNIKOW PROBLEM ON A CLASS OF ADDITIVELY IDEMPOTENT SEMIRINGS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 05 September 2013, pp. 404-420
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
IRREDUCIBLE QUASIORDERS OF MONOUNARY ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 01 March 2013, pp. 259-276
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
Perfect effect algebras are categorically equivalent with Abelian interpolation po-groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 2 / April 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 183-207
- Print publication:
- April 2007
-
- Article
-
- You have access
- Export citation
Infinitary lattice and Riesz properties of pseudoeffect algebras and po-groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 3 / December 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 295-312
- Print publication:
- December 2003
-
- Article
-
- You have access
- Export citation
On Products in Lattice-ordered Algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 1 / August 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 23-40
- Print publication:
- August 2003
-
- Article
-
- You have access
- Export citation