Refine listing
Actions for selected content:
105 results in 34Bxx
Dependence of the Weyl coefficient on singular interface conditions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 28 May 2009, pp. 445-487
-
- Article
-
- You have access
- Export citation
Existence results for nonlinear periodic boundary-value problems
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 02 February 2009, pp. 79-95
-
- Article
-
- You have access
- Export citation
POSITIVE PERIODIC SOLUTIONS OF SECOND-ORDER DIFFERENTIAL EQUATIONS WITH SINGULARITIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 163-169
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
SUCCESSIVE ITERATION AND POSITIVE SOLUTIONS FOR A p-LAPLACIAN MULTIPOINT BOUNDARY VALUE PROBLEM
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 4 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 551-560
-
- Article
-
- You have access
- Export citation
THREE NONNEGATIVE SOLUTIONS FOR SECOND-ORDER IMPULSIVE DIFFERENTIAL EQUATIONS WITH A THREE-POINT BOUNDARY VALUE PROBLEM
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 3 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 337-346
-
- Article
-
- You have access
- Export citation
Multiplicities of eigenvalues of a vector-valued Sturm-Liouville problem
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 119-127
- Print publication:
- June 2002
-
- Article
- Export citation
Continuous and discrete boundary value problems on the infinite interval: existence theory
- Part of
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 273-292
- Print publication:
- December 2001
-
- Article
- Export citation
Bounds for the points of spectral concentration of Sturm–Liouville problems
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 327-337
- Print publication:
- December 2000
-
- Article
- Export citation
The convexity of the spectral function in Sturm–Liouville problems
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 319-326
- Print publication:
- December 2000
-
- Article
- Export citation
Solvability in Lp of the Neumann problem for a singular non-homogeneous Sturm-Liouville equation
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 2 / December 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 453-470
- Print publication:
- December 1999
-
- Article
- Export citation
A Global algorithm for geodesics
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 1 / August 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 37-50
- Print publication:
- August 1998
-
- Article
-
- You have access
- Export citation
On the location of spectral concentration for Sturm–Liouville problems with rapidly decaying potential
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 1 / June 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 25-36
- Print publication:
- June 1998
-
- Article
- Export citation
The form of the spectral functions associated with Sturm-Liouville problems with continuous spectrum
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 1 / June 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 149-161
- Print publication:
- June 1997
-
- Article
- Export citation
The asymptotic form of the Titchmarsh-weyl m-function associated with a non-definite, linear, second order differential equation
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 1 / June 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 209-222
- Print publication:
- June 1996
-
- Article
- Export citation
Solvability of semilinear abstract equations at resonance
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 2 / December 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 301-311
- Print publication:
- December 1994
-
- Article
- Export citation
Existence results for differential equations with reflection of the argument
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 2 / October 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 237-260
- Print publication:
- October 1994
-
- Article
-
- You have access
- Export citation
Saddle point theorem and nonlinear scalar Neumann boundary value problems
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 55 / Issue 3 / December 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 386-402
- Print publication:
- December 1993
-
- Article
-
- You have access
- Export citation
Bifurcation of steady-state solutions of a scalar reaction-diffusion equation in one space variable
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 52 / Issue 3 / June 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 343-355
- Print publication:
- June 1992
-
- Article
-
- You have access
- Export citation
Bifurcation and stability of positive solutions of a two-point boundary value problem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 52 / Issue 3 / June 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 334-342
- Print publication:
- June 1992
-
- Article
-
- You have access
- Export citation
A generalization of Rolle's Theorem and an application to a nonlinear equation
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 46 / Issue 3 / June 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 395-401
- Print publication:
- June 1989
-
- Article
-
- You have access
- Export citation
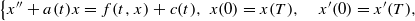
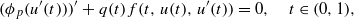
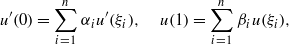
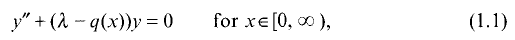
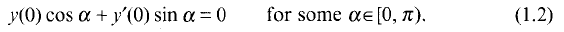
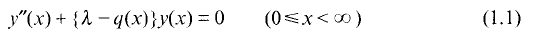
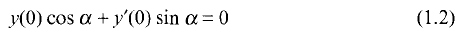
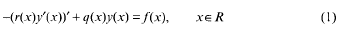
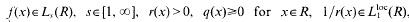 ,
, 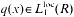 . The inversion problem for (1) is called regular in
. The inversion problem for (1) is called regular in 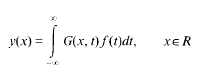
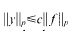 . Here
. Here 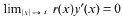 for any
for any 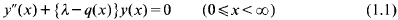
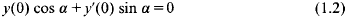
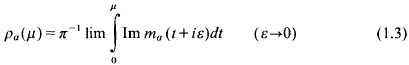
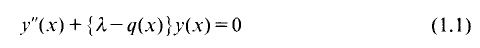
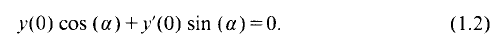

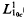 (0, ∞) and λ is a complex number with
(0, ∞) and λ is a complex number with
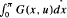 (for¦
(for¦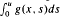 is the potential generated by
is the potential generated by 