In this paper we study impulsive periodic solutions for second-order nonautonomous singular differential equations. Our proof is based on the mountain pass theorem. Some recent results in the literature are extended.

By modifying the inner product in the direct sum of the Hilbert spaces associated with each of two underlying intervals on which an even-order equation is defined, we generate self-adjoint realisations for boundary conditions with any real coupling matrix which are much more general than the coupling matrices from the ‘unmodified’ theory.

The homotopy analysis method (HAM) is applied to a nonlinear ordinary differential equation (ODE) emerging from a closure model of the von Kármán–Howarth equation which models the decay of isotropic turbulence. In the infinite Reynolds number limit, the von Kármán–Howarth equation admits a symmetry reduction leading to the aforementioned one-parameter ODE. Though the latter equation is not fully integrable, it can be integrated once for two particular parameter values and, for one of these values, the relevant boundary conditions can also be satisfied. The key result of this paper is that for the generic case, HAM is employed such that solutions for arbitrary parameter values are derived. We obtain explicit analytical solutions by recursive formulas with constant coefficients, using some transformations of variables in order to express the solutions in polynomial form. We also prove that the Loitsyansky invariant is a conservation law for the asymptotic form of the original equation.

Existence results of positive solutions for a two point boundary value problem are established. No asymptotic condition on the nonlinear term either at zero or at infinity is required. A classical result of Erbe and Wang is improved. The approach is based on variational methods.

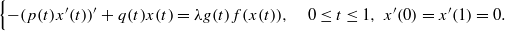
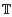We study classes of higher-order singular boundary-value problems on a time scale with a positive parameter λ in the differential equations. A homeomorphism and homomorphism ø are involved both in the differential equation and in the boundary conditions. Criteria are obtained for the existence and uniqueness of positive solutions. The dependence of positive solutions on the parameter λ is studied. Applications of our results to special problems are also discussed. Our analysis mainly relies on the mixed monotone operator theory. The results here are new, even in the cases of second-order differential and difference equations.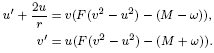

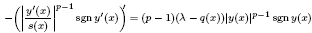
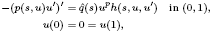
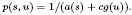
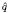By making use of Merle's general shooting method we investigate Dirac equations of the form

Here it is possible that F(0) = −∞ and that F(s) defined on (0,+∞) is not monotonously nondecreasing. Our results cover some known ones as a special case.

In this paper, we deal with the multiplicity of solutions for a fourth-order impulsive differential equation with a parameter. Using variational methods and a ‘three critical points’ theorem, we give some new criteria to guarantee that the impulsive problem has at least three classical solutions. An example is also given in order to illustrate the main results.

We prove that the eigenvalues of a certain highly non-self-adjoint operator that arises in fluid mechanics correspond, up to scaling by a positive constant, to those of a self-adjoint operator with compact resolvent; hence there are infinitely many real eigenvalues which accumulate only at ±∞. We use this result to determine the asymptotic distribution of the eigenvalues.

The nonlinear eigenvalue problem

for 0 ≤ x < ∞, fixed p ∈ (1, ∞), and with y′(0)/y(0) specified is studied under various conditions on the coefficients s and q, leading to either oscillatory or non-oscillatory situations.

We establish new sampling representations for linear integral transforms associated with arbitrary general Birkhoff regular boundary value problems. The new approach is developed in connection with the analytical properties of Green’s function, and does not require the root functions to be a basis or complete. Unlike most of the known sampling expansions associated with eigenvalue problems, the results obtained are, generally speaking, of Hermite interpolation type.

We study the existence of multiple solutions for a two-point boundary-value problem associated with a planar system of second-order ordinary differential equations by using a shooting technique. We consider asymptotically linear nonlinearities satisfying suitable sign conditions. Multiplicity is ensured by assumptions involving the Morse indices of the linearizations at zero and at infinity.

The upper and lower solutions method and Leray–Schauder degree theory are employed to establish the existence result for a class of nonlinear third-order two-point boundary-value problems with a sign-type Nagumo condition.

This paper is concerned with a boundary-value problem on the half-line for nonlinear two-dimensional delay differential systems with positive delays. A theorem is established, which provides sufficient conditions for the existence of positive solutions. The application of this theorem to the special case of second-order nonlinear delay differential equations is given. Also, the application of the theorem to two-dimensional Emden–Fowler-type delay differential systems with constant delays is presented. Moreover, some general examples demonstrating the applicability of the theorem are included.

We establish the existence of positive solutions of the Sturm–Liouville problem

where

We assume g and to be non-negative, continuous functions, a(s) is a positive continuous function, c≥0, p>1, and the function h is sub-quadratic with respect to u′. We combine a priori estimates with a fixed-point result of Krasnosel'skii to obtain the existence of a positive solution.

A class of first-order impulsive functional differential equations with forcing terms is considered. It is shown that, under certain assumptions, there exist positive T-periodic solutions, and under some other assumptions, there exists no positive T-periodic solution. Applications and examples are given to illustrate the main results.

In this paper, we consider the existence of nontrivial solutions for the nonlinear fractional differential equation boundary-value problem (BVP) where 1<α≤2, η∈(0,1),β∈ℝ=(−∞,+∞), βηα−1≠1, Dα is the Riemann–Liouville differential operator of order α, and f:[0,1]×ℝ→ℝ is continuous, q(t):[0,1]→[0,+∞) is Lebesgue integrable. We give some sufficient conditions for the existence of nontrivial solutions to the above boundary-value problems. Our approach is based on the Leray–Schauder nonlinear alternative. Particularly, we do not use the nonnegative assumption and monotonicity on f which was essential for the technique used in almost all existed literature.

We investigate the influence of interface conditions at a singularity of an indefinite canonical system on its Weyl coefficient. An explicit formula which parametrizes all possible Weyl coefficients of indefinite canonical systems with fixed Hamiltonian function is derived. This result is illustrated with two examples: the Bessel equation, which has a singular end point, and a Sturm–Liouville equation whose potential has an inner singularity, which arises from a continuation problem for a positive definite function.

We study a class of second-order nonlinear differential equations on a finite interval with periodic boundary conditions. The nonlinearity in the equations can take negative values and may be unbounded from below. Criteria are established for the existence of non-trivial solutions, positive solutions and negative solutions of the problems under consideration. Applications of our results to related eigenvalue problems are also discussed. Examples are included to illustrate some of the results. Our analysis relies mainly on topological degree theory.

In this work, we consider the periodic boundary value problem where a,c∈L1(0,T) and f is a Carathéodory function. An existence theorem for positive periodic solutions is proved in the case where the associated Green function is nonnegative. Our result is valid for systems with strong singularities, and answers partially the open problem raised in Torres [‘Weak singularities may help periodic solutions to exist’, J. Differential Equations232 (2007), 277–284].

In this paper, we study the existence of positive solutions for the one-dimensional p-Laplacian differential equation, subject to the multipoint boundary condition by applying a monotone iterative method.