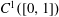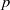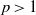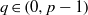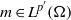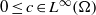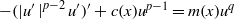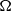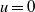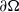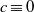Refine listing
Actions for selected content:
105 results in 34Bxx
A bifurcation diagram of solutions to an elliptic equation with exponential nonlinearity in higher dimensions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 17 October 2017, pp. 101-122
- Print publication:
- February 2018
-
- Article
- Export citation
Partial inverse problems for Sturm–Liouville operators on trees
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 5 / October 2017
- Published online by Cambridge University Press:
- 15 August 2017, pp. 917-933
- Print publication:
- October 2017
-
- Article
- Export citation
Discreteness of spectrum for Schrödinger operators with δʹ-type conditions on infinite regular trees
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 5 / October 2017
- Published online by Cambridge University Press:
- 14 August 2017, pp. 1091-1117
- Print publication:
- October 2017
-
- Article
- Export citation
Geometric aspects of self-adjoint Sturm–Liouville problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 6 / December 2017
- Published online by Cambridge University Press:
- 14 August 2017, pp. 1279-1295
- Print publication:
- December 2017
-
- Article
- Export citation
Second-order differential equations with random perturbations and small parameters
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 05 July 2017, pp. 763-779
- Print publication:
- August 2017
-
- Article
- Export citation
EXISTENCE OF POSITIVE SOLUTION FOR INDEFINITE KIRCHHOFF EQUATION IN EXTERIOR DOMAINS WITH SUBCRITICAL OR CRITICAL GROWTH
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 23 December 2016, pp. 329-340
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
Borg's Periodicity Theorems for First-Order Self-Adjoint Systems with Complex Potentials
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 19 December 2016, pp. 615-633
-
- Article
- Export citation
On Semipositone Non-Local Boundary-Value Problems with Nonlinear or Affine Boundary Conditions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 02 November 2016, pp. 635-649
-
- Article
- Export citation
A Fully Discrete Spectral Method for Fisher’s Equation on the Whole Line
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 6 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 19 October 2016, pp. 400-415
- Print publication:
- November 2016
-
- Article
- Export citation
Pairs of positive periodic solutions of nonlinear ODEs with indefinite weight: a topological degree approach for the super–sublinear case
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 16 May 2016, pp. 449-474
- Print publication:
- June 2016
-
- Article
- Export citation
A criterion for compactness in Lp(ℝ) of the resolvent of the maximal general form Sturm–Liouville operator
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 19 April 2016, pp. 483-508
- Print publication:
- June 2016
-
- Article
- Export citation
DIFFERENTIATING SOLUTIONS OF A BOUNDARY VALUE PROBLEM ON A TIME SCALE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 01 April 2016, pp. 101-109
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
Non-trivial solutions of local and non-local Neumann boundary-value problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 07 March 2016, pp. 337-369
- Print publication:
- April 2016
-
- Article
- Export citation
Boundary-Value Problems for Third-Order Lipschitz Ordinary Differential Equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 28 October 2014, pp. 183-197
-
- Article
-
- You have access
- Export citation
On Nonlinear Boundary Conditions Involving Decomposable Linear Functionals
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 27 October 2014, pp. 421-439
-
- Article
-
- You have access
- Export citation
DEPENDENCE OF EIGENVALUES OF SIXTH-ORDER BOUNDARY VALUE PROBLEMS ON THE BOUNDARY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 09 September 2014, pp. 457-468
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
SUCCESSIVE ITERATIONS FOR POSITIVE EXTREMAL SOLUTIONS OF NONLINEAR FRACTIONAL DIFFERENTIAL EQUATIONS ON A HALF-LINE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 27 August 2014, pp. 116-128
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
A VARIATIONAL APPROACH FOR ONE-DIMENSIONAL PRESCRIBED MEAN CURVATURE PROBLEMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 25 July 2014, pp. 145-161
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
STRICTLY POSITIVE SOLUTIONS FOR ONE-DIMENSIONAL NONLINEAR PROBLEMS INVOLVING THE
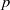 $p$-LAPLACIAN
$p$-LAPLACIAN
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 06 September 2013, pp. 243-251
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
Solutions and multiple solutions for superlinear perturbations of the periodic scalar p-Laplacian
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 3 / October 2013
- Published online by Cambridge University Press:
- 28 June 2013, pp. 805-827
-
- Article
-
- You have access
- Export citation
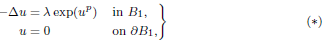
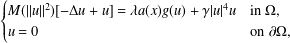
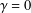
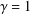
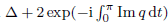 are double zeros if and only if this self-adjoint system is unitarily equivalent to one in which
are double zeros if and only if this self-adjoint system is unitarily equivalent to one in which 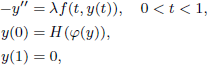
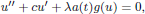
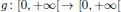 is a sublinear function at infinity having superlinear growth at zero. We prove the existence of two positive solutions when
is a sublinear function at infinity having superlinear growth at zero. We prove the existence of two positive solutions when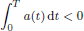
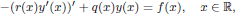
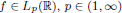 and
and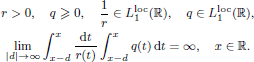
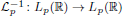 of the maximal continuously invertible Sturm–Liouville operator
of the maximal continuously invertible Sturm–Liouville operator 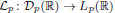 . Here
. Here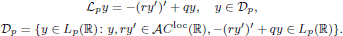
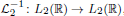 , we obtain two-sided sharp-by-order estimates of the maximal eigenvalue.
, we obtain two-sided sharp-by-order estimates of the maximal eigenvalue.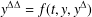
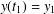
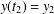
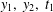
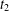
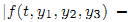
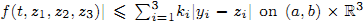 , questions involving ‘uniqueness implies uniqueness’, ‘uniqueness implies existence’ and ‘optimal length subintervals of (
, questions involving ‘uniqueness implies uniqueness’, ‘uniqueness implies existence’ and ‘optimal length subintervals of (