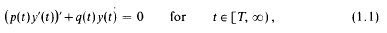Refine listing
Actions for selected content:
112 results in 34Cxx
Some results on the asymptotic behavior of nonoscillatory solutions of differential equations with deviating arguments
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 32 / Issue 3 / June 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 295-317
-
- Article
-
- You have access
- Export citation
An extension of the principle of spatial averaging for inertial manifolds
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 1 / February 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 125-142
-
- Article
-
- You have access
- Export citation
Oscillation of a functional differential equation arising from an industrial problem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 26 / Issue 3 / November 1978
- Published online by Cambridge University Press:
- 09 April 2009, pp. 323-329
-
- Article
-
- You have access
- Export citation
Admissible solutions of the Schwarzian differential equation
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 2 / April 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 258-278
-
- Article
-
- You have access
- Export citation
Iterative criteria for bounds on the growth of positive solutions of a delay differential equation
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 25 / Issue 2 / March 1978
- Published online by Cambridge University Press:
- 09 April 2009, pp. 195-200
-
- Article
-
- You have access
- Export citation
Sufficient conditions for the strong stability of the differential equation [p(D)+f(t)q(D)]y = 0
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 2 / October 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 280-299
-
- Article
-
- You have access
- Export citation
On non-homogeneous canonical third-order linear differential equations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 2 / October 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 138-148
-
- Article
-
- You have access
- Export citation
OSCILLATION OF SOLUTIONS OF LINEAR DIFFERENTIAL EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 09 February 2009, pp. 161-169
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation
Averaging analysis of a point process adaptive algorithm
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue A / 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 361-372
- Print publication:
- 2004
-
- Article
- Export citation
Comparison theorems of Sturm's type
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 2 / December 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 312-321
- Print publication:
- December 1994
-
- Article
- Export citation
On the asymptotic properties of linear differential equations
- Part of
-
- Journal:
- Mathematika / Volume 34 / Issue 2 / December 1987
- Published online by Cambridge University Press:
- 26 February 2010, pp. 187-198
- Print publication:
- December 1987
-
- Article
- Export citation
On the oscillation of solutions of linear differential equations
- Part of
-
- Journal:
- Mathematika / Volume 31 / Issue 2 / December 1984
- Published online by Cambridge University Press:
- 26 February 2010, pp. 214-226
- Print publication:
- December 1984
-
- Article
- Export citation
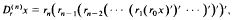
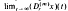 exists in R – {0} The results obtained extend some recent ones due to Philos (1978a) and they prove, in a general setting, the validity of a conjecture made by Kusano and Onose (1975).
exists in R – {0} The results obtained extend some recent ones due to Philos (1978a) and they prove, in a general setting, the validity of a conjecture made by Kusano and Onose (1975).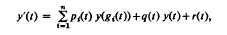
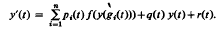

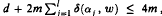 , where α
, where α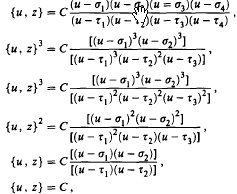
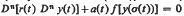 are classified according to types
are classified according to types 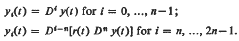
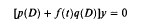 where the continuous function
where the continuous function 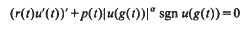
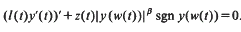
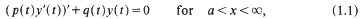
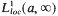 with
with