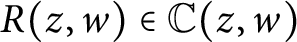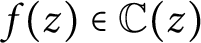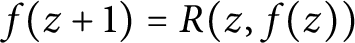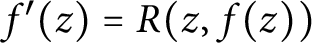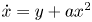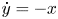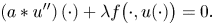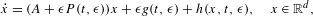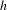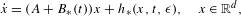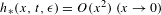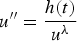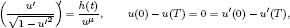Refine listing
Actions for selected content:
112 results in 34Cxx
Effective finiteness of solutions to certain differential and difference equations
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 16 February 2021, pp. 52-67
- Print publication:
- March 2022
-
- Article
- Export citation
The cyclicity of the period annulus of a reversible quadratic system
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 10 February 2021, pp. 281-290
- Print publication:
- April 2022
-
- Article
- Export citation
Realization of analytic moduli for parabolic Dulac germs
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 18 January 2021, pp. 195-249
- Print publication:
- January 2022
-
- Article
- Export citation
Existence and monotonicity of nonlocal boundary value problems: the one-dimensional case
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 23 December 2020, pp. 1-27
- Print publication:
- February 2022
-
- Article
- Export citation
Bloch wave homogenisation of quasiperiodic media
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 05 October 2020, pp. 58-78
-
- Article
- Export citation
Isolas of multi-pulse solutions to lattice dynamical systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 20 July 2020, pp. 916-952
- Print publication:
- June 2021
-
- Article
- Export citation
THE PARADOX OF ENRICHMENT, SPATIAL HETEROGENEITY, COMMUNITY EFFECTS AND THE PHENOMENON OF APPARENT DISAPPEARANCE IN THE MARINE BACTERIOPHAGE DYNAMICS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 62 / Issue 4 / October 2020
- Published online by Cambridge University Press:
- 22 June 2020, pp. 453-468
-
- Article
-
- You have access
- Export citation
On the birth and death of algebraic limit cycles in quadratic differential systems
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 26 May 2020, pp. 317-336
-
- Article
- Export citation
Reducibility of a class of nonlinear quasi-periodic systems with Liouvillean basic frequencies
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 09 March 2020, pp. 1883-1920
- Print publication:
- June 2021
-
- Article
- Export citation
On the Poincaré problem and Liouvillian integrability of quadratic Liénard differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 09 January 2020, pp. 3231-3251
- Print publication:
- December 2020
-
- Article
- Export citation
Stability of Almost Periodic Nicholson’s Blowflies Model Involving Patch Structure and Mortality Terms
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 23 December 2019, pp. 405-422
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
On Periodic Solutions to Constrained Lagrangian System
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 18 December 2019, pp. 242-255
- Print publication:
- March 2020
-
- Article
-
- You have access
- Export citation
Limit Cycles of a Perturbation of a Polynomial Hamiltonian Systems of Degree 4 Symmetric with Respect to the Origin
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 18 October 2019, pp. 547-561
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
Oscillation Criteria for Second Order Ordinary Differential Equations
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 13 September 2019, pp. 276-286
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Hilbert’s 16th problem on a period annulus and Nash space of arcs
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 2 / September 2020
- Published online by Cambridge University Press:
- 12 July 2019, pp. 377-409
- Print publication:
- September 2020
-
- Article
- Export citation
Fixed points of multivalued maps under local Lipschitz conditions and applications
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 1467-1494
- Print publication:
- June 2020
-
- Article
- Export citation
Periodic solutions for a second-order differential equation with indefinite weak singularity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 15 January 2019, pp. 1135-1152
- Print publication:
- October 2019
-
- Article
- Export citation
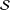 ${\mathcal{S}}$ -ASYMPTOTICALLY PERIODIC SOLUTIONS FOR ABSTRACT EQUATIONSWITH STATE-DEPENDENT DELAY
${\mathcal{S}}$ -ASYMPTOTICALLY PERIODIC SOLUTIONS FOR ABSTRACT EQUATIONSWITH STATE-DEPENDENT DELAY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 15 August 2018, pp. 456-464
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
Periodic solutions for indefinite singular perturbations of the relativistic acceleration
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 4 / August 2018
- Published online by Cambridge University Press:
- 22 June 2018, pp. 703-712
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
The non-existence, existence and uniqueness of limit cycles for quadratic polynomial differential systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 20 November 2017, pp. 1-14
- Print publication:
- February 2019
-
- Article
- Export citation