Refine listing
Actions for selected content:
110 results in 34Cxx
Convexity-preserving flows of totally competitive planar Lotka–Volterra equations and the geometry of the carrying simplex
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 01 November 2011, pp. 53-63
-
- Article
-
- You have access
- Export citation
WEIGHTED PSEUDO-ALMOST PERIODIC SOLUTIONS FOR SOME ABSTRACT DIFFERENTIAL EQUATIONS WITH UNIFORM CONTINUITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 13 October 2010, pp. 424-436
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
A NOTE ON PERIODIC SOLUTIONS OF A FORCED LIÉNARD-TYPE EQUATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 51 / Issue 3 / January 2010
- Published online by Cambridge University Press:
- 27 September 2010, pp. 350-368
-
- Article
-
- You have access
- Export citation
PERIODIC SOLUTIONS OF SINGULAR DIFFERENTIAL EQUATIONS WITH SIGN-CHANGING POTENTIAL
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 14 September 2010, pp. 437-445
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
Centre manifold variety for eight-parameter families of polynomial vector fields of arbitrary degree
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 30 April 2010, pp. 511-530
-
- Article
-
- You have access
- Export citation
Unstable sets, heteroclinic orbits and generic quasi-convergence for essentially strongly order-preserving semiflows
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 3 / October 2009
- Published online by Cambridge University Press:
- 23 September 2009, pp. 797-807
-
- Article
-
- You have access
- Export citation
FURTHER RESULTS ON POSITIVE PERIODIC SOLUTIONS OF IMPULSIVE FUNCTIONAL DIFFERENTIAL EQUATIONS AND APPLICATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 4 / April 2009
- Published online by Cambridge University Press:
- 27 July 2009, pp. 513-533
-
- Article
-
- You have access
- Export citation
EXISTENCE AND STABILITY OF PERIODIC SOLUTIONS OF A RAYLEIGH TYPE EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 3 / June 2009
- Published online by Cambridge University Press:
- 17 April 2009, pp. 377-390
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
OSCILLATION OF SOLUTIONS OF LINEAR DIFFERENTIAL EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 09 February 2009, pp. 161-169
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation
Averaging analysis of a point process adaptive algorithm
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue A / 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 361-372
- Print publication:
- 2004
-
- Article
- Export citation
The number of limit cycles for a class of quintic Hamiltonian systems under quintic perturbations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 1 / August 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 37-54
- Print publication:
- August 2002
-
- Article
-
- You have access
- Export citation
An extension of the principle of spatial averaging for inertial manifolds
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 1 / February 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 125-142
- Print publication:
- February 1999
-
- Article
-
- You have access
- Export citation
Generalized theorem of Hartman-Grobman on measure chains
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 2 / April 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 157-191
- Print publication:
- April 1996
-
- Article
-
- You have access
- Export citation
Comparison theorems of Sturm's type
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 2 / December 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 312-321
- Print publication:
- December 1994
-
- Article
- Export citation
On non-homogeneous canonical third-order linear differential equations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 2 / October 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 138-148
- Print publication:
- October 1994
-
- Article
-
- You have access
- Export citation
Oscillation theorems for second order superlinear differential equations with damping
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 53 / Issue 2 / October 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 156-165
- Print publication:
- October 1992
-
- Article
-
- You have access
- Export citation
Oscillations of higher order neutral differential equations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 52 / Issue 2 / April 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 261-284
- Print publication:
- April 1992
-
- Article
-
- You have access
- Export citation
Admissible solutions of the Schwarzian differential equation
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 2 / April 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 258-278
- Print publication:
- April 1991
-
- Article
-
- You have access
- Export citation
Oscillation criteria for second order differential equations with damping
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 1 / August 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 43-54
- Print publication:
- August 1990
-
- Article
-
- You have access
- Export citation
Sufficient conditions for the strong stability of the differential equation [p(D)+f(t)q(D)]y = 0
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 2 / October 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 280-299
- Print publication:
- October 1989
-
- Article
-
- You have access
- Export citation
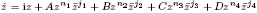 , where
, where 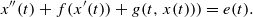
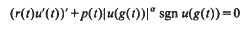
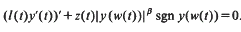
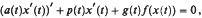
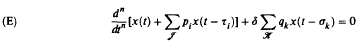
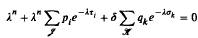

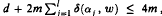 , where α
, where α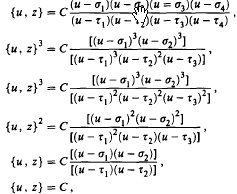
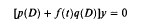 where the continuous function
where the continuous function 