Refine listing
Actions for selected content:
112 results in 34Cxx
SEMI-ANALYTICAL SOLUTIONS FOR THE BRUSSELATOR REACTION–DIFFUSION MODEL
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 59 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 23 October 2017, pp. 167-182
-
- Article
-
- You have access
- Export citation
DYNAMICS OF MATHEMATICAL MODELS FOR BIOREACTORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 28 September 2017, pp. 519-520
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
Dynamics of an Innovation Diffusion Model with Time Delay
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 07 September 2017, pp. 455-481
- Print publication:
- August 2017
-
- Article
- Export citation
Second-order differential equations with random perturbations and small parameters
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 05 July 2017, pp. 763-779
- Print publication:
- August 2017
-
- Article
- Export citation
Adapted Nested Force-Gradient Integrators: The Schwinger Model Case
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 4 / April 2017
- Published online by Cambridge University Press:
- 08 March 2017, pp. 1141-1153
- Print publication:
- April 2017
-
- Article
- Export citation
DYNAMICS OF PSEUDO ALMOST PERIODIC SOLUTION FOR IMPULSIVE NEOCLASSICAL GROWTH MODEL
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 06 March 2017, pp. 359-367
-
- Article
-
- You have access
- Export citation
Modification and Numerical Method for the Jiles-Atherton Hysteresis Model
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 3 / March 2017
- Published online by Cambridge University Press:
- 07 February 2017, pp. 763-781
- Print publication:
- March 2017
-
- Article
- Export citation
EXISTENCE OF POSITIVE SOLUTION FOR INDEFINITE KIRCHHOFF EQUATION IN EXTERIOR DOMAINS WITH SUBCRITICAL OR CRITICAL GROWTH
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 23 December 2016, pp. 329-340
-
- Article
-
- You have access
- Export citation
Connecting orbits for a class of singular time-periodic second-order Hamiltonian systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 6 / December 2016
- Published online by Cambridge University Press:
- 08 November 2016, pp. 1211-1241
- Print publication:
- December 2016
-
- Article
- Export citation
Pairs of positive periodic solutions of nonlinear ODEs with indefinite weight: a topological degree approach for the super–sublinear case
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 16 May 2016, pp. 449-474
- Print publication:
- June 2016
-
- Article
- Export citation
Computational Study of Traveling Wave Solutions of Isothermal Chemical Systems
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 17 May 2016, pp. 1461-1472
- Print publication:
- May 2016
-
- Article
- Export citation
On the loss of compactness in the vectorial heteroclinic connection problem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 22 March 2016, pp. 595-608
- Print publication:
- June 2016
-
- Article
- Export citation
On strongly decreasing solutions of cyclic systems of second-order nonlinear differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 5 / October 2015
- Published online by Cambridge University Press:
- 02 September 2015, pp. 1007-1028
- Print publication:
- October 2015
-
- Article
- Export citation
CANARDS IN ADVECTION–REACTION–DIFFUSION SYSTEMS IN ONE SPATIAL DIMENSION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 16 June 2015, pp. 342-343
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
ANALYTIC REDUCIBILITY OF RESONANT COCYCLES TO A NORMAL FORM
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 27 November 2014, pp. 203-223
- Print publication:
- January 2016
-
- Article
- Export citation
Weighted Estimates for Solutions of the General Sturm-Liouville Equation and the Everitt-Giertz Problem. I
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 21 July 2014, pp. 125-147
-
- Article
-
- You have access
- Export citation
Solutions and multiple solutions for superlinear perturbations of the periodic scalar p-Laplacian
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 3 / October 2013
- Published online by Cambridge University Press:
- 28 June 2013, pp. 805-827
-
- Article
-
- You have access
- Export citation
CALCULUS FROM THE PAST: MULTIPLE DELAY SYSTEMS ARISING IN CANCER CELL MODELLING
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 54 / Issue 3 / January 2013
- Published online by Cambridge University Press:
- 30 April 2013, pp. 117-126
-
- Article
-
- You have access
- Export citation
Generalized ‘second Ritt theorem’ and explicit solution of the polynomial moment problem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 4 / April 2013
- Published online by Cambridge University Press:
- 29 January 2013, pp. 705-728
- Print publication:
- April 2013
-
- Article
- Export citation
ON THE NUMBER OF LIMIT CYCLES IN PERTURBATIONS OF A QUADRATIC REVERSIBLE CENTER
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 11 October 2012, pp. 409-423
-
- Article
-
- You have access
- Export citation
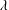
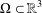
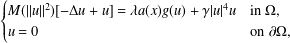
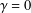
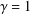
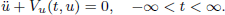
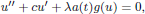
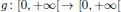 is a sublinear function at infinity having superlinear growth at zero. We prove the existence of two positive solutions when
is a sublinear function at infinity having superlinear growth at zero. We prove the existence of two positive solutions when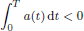
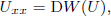
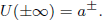
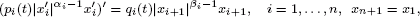


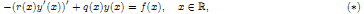
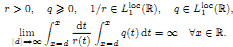
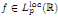 , there exists a unique solution
, there exists a unique solution 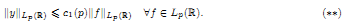
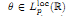 be given. We have to find minimal additional restrictions for
be given. We have to find minimal additional restrictions for