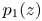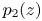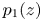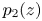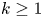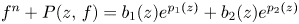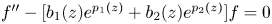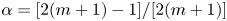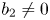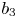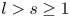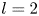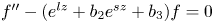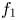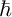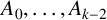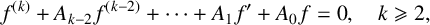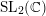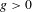Refine listing
Actions for selected content:
38 results in 34Mxx
Spherical normal forms for germs of parabolic line biholomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 07 April 2025, pp. 3255-3304
- Print publication:
- October 2025
-
- Article
- Export citation
Complex linear differential equations with solutions in weighted Dirichlet spaces and derivative Hardy spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 06 January 2025, pp. 653-666
- Print publication:
- September 2025
-
- Article
- Export citation
EXPONENTIAL ASYMPTOTICS USING NUMERICAL RATIONAL APPROXIMATION IN LINEAR DIFFERENTIAL EQUATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 65 / Issue 4 / October 2023
- Published online by Cambridge University Press:
- 22 April 2024, pp. 285-307
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-integrability of the restricted three-body problem
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 3012-3040
- Print publication:
- October 2024
-
- Article
- Export citation
From topological recursion to wave functions and PDEs quantizing hyperelliptic curves
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 31 October 2023, e99
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global Asymptotics of the Sixth Painlevé Equation in Okamoto’s Space
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 13 March 2023, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PILOT-WAVE HYDRODYNAMICS: QUANTISATION OF PARTIAL INTEGRABILITY FROM A NONLINEAR INTEGRO-DIFFERENTIAL EQUATION OF THE SECOND ORDER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 27 February 2023, pp. 472-479
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A fixed-point curve theorem for finite-orbits local diffeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 12 / December 2023
- Published online by Cambridge University Press:
- 16 February 2023, pp. 4138-4165
- Print publication:
- December 2023
-
- Article
- Export citation
On the oscillation of certain second-order linear differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 09 December 2022, pp. 1965-1992
- Print publication:
- December 2023
-
- Article
- Export citation
EXACT SOLUTIONS FOR THE SINGULARLY PERTURBED RICCATI EQUATION AND EXACT WKB ANALYSIS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 250 / June 2023
- Published online by Cambridge University Press:
- 08 December 2022, pp. 434-469
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DESCRIPTION OF GROWTH AND OSCILLATION OF SOLUTIONS OF COMPLEX LDE’S
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 16 June 2022, pp. 145-171
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE MODULARITY OF SOLUTIONS TO CERTAIN DIFFERENTIAL EQUATIONS OF HYPERGEOMETRIC TYPE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 15 September 2021, pp. 385-391
- Print publication:
- June 2022
-
- Article
- Export citation
NOTES ON VANISHING CYCLES AND APPLICATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 29 October 2020, pp. 371-415
- Print publication:
- December 2020
-
- Article
- Export citation
q-DISCRETE PAINLEVÉ EQUATIONS: THEIR HIERARCHIES AND PROPERTIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 14 September 2020, pp. 333-334
- Print publication:
- April 2021
-
- Article
-
- You have access
- Export citation
On the number of linearly independent admissible solutions to linear differential and linear difference equations
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 30 July 2020, pp. 1556-1591
- Print publication:
- December 2021
-
- Article
- Export citation
Classification of algebraic solutions of irregular Garnier systems
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 5 / May 2020
- Published online by Cambridge University Press:
- 14 April 2020, pp. 881-907
- Print publication:
- May 2020
-
- Article
- Export citation
ALGEBRAIC ISOMONODROMIC DEFORMATIONS AND THE MAPPING CLASS GROUP
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 18 November 2019, pp. 1497-1545
- Print publication:
- September 2021
-
- Article
- Export citation
QUANTITATIVE PROPERTIES OF MEROMORPHIC SOLUTIONS TO SOME DIFFERENTIAL-DIFFERENCE EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 26 December 2018, pp. 250-261
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
Parametric rigidity of real families of conformal diffeomorphisms tangent to x→−x
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 30 August 2018, pp. 261-277
- Print publication:
- February 2019
-
- Article
- Export citation
SHIDLOVSKY’S MULTIPLICITY ESTIMATE AND IRRATIONALITY OF ZETA VALUES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 105 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 18 June 2018, pp. 145-172
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation