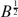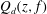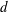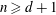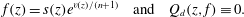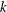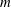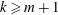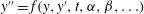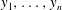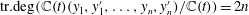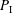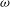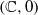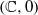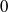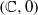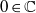Refine listing
Actions for selected content:
38 results in 34Mxx
RIGID LOCAL SYSTEMS ON
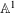 $\mathbb{A}^{1}$ WITH FINITE MONODROMY
$\mathbb{A}^{1}$ WITH FINITE MONODROMY
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 3 / 2018
- Published online by Cambridge University Press:
- 01 August 2018, pp. 785-846
- Print publication:
- 2018
-
- Article
- Export citation
ON ALGEBRAIC DIFFERENTIAL EQUATIONS FOR THE GAMMA FUNCTION AND
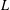 $L$ -FUNCTIONS IN THE EXTENDED SELBERG CLASS
$L$ -FUNCTIONS IN THE EXTENDED SELBERG CLASS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 36-43
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
HYPERTRANSCENDENCE OF
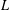 $L$-FUNCTIONS FOR
$L$-FUNCTIONS FOR 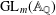 $\text{GL}_{m}(\mathbb{A}_{\mathbb{Q}})$
$\text{GL}_{m}(\mathbb{A}_{\mathbb{Q}})$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 11 November 2015, pp. 388-399
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
LOCALISATION OF LINEAR DIFFERENTIAL EQUATIONS IN THE UNIT DISC BY A CONFORMAL MAP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 15 October 2015, pp. 260-271
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
ON THE BRÜCK CONJECTURE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 02 October 2015, pp. 248-259
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
Semiclassical orthogonal polynomial systems on nonuniform lattices, deformations of the Askey table, and analogues of isomonodromy
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 219 / September 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 127-234
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
ON UNICITY OF MEROMORPHIC SOLUTIONS TO DIFFERENCE EQUATIONS OF MALMQUIST TYPE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 05 August 2015, pp. 92-98
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
DIFFERENCE ALGEBRAIC RELATIONS AMONG SOLUTIONS OF LINEAR DIFFERENTIAL EQUATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 17 April 2015, pp. 59-119
- Print publication:
- February 2017
-
- Article
- Export citation
ON THE ESCAPING SET OF MEROMORPHIC FUNCTIONS WITH DIRECT TRACTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 02 April 2015, pp. 68-76
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
ON THE COMPLEXITY OF FINDING A NECESSARY AND SUFFICIENT CONDITION FOR BLASCHKE-OSCILLATORY EQUATIONS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 17 December 2014, pp. 543-554
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
ON SOLUTIONS TO NONHOMOGENEOUS ALGEBRAIC DIFFERENTIAL EQUATIONS AND THEIR APPLICATION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 24 September 2014, pp. 391-403
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
On the algebraic independence of generic Painlevé transcendents
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 4 / April 2014
- Published online by Cambridge University Press:
- 10 March 2014, pp. 668-678
- Print publication:
- April 2014
-
- Article
- Export citation
Cyclic stabilizers and infinitely many hyperbolic orbits for pseudogroups on
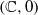 $( \mathbb{C} , 0)$
$( \mathbb{C} , 0)$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 06 August 2013, pp. 413-446
- Print publication:
- April 2014
-
- Article
- Export citation
Unipotent differential algebraic groups as parameterized differential Galois groups
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 4 / October 2014
- Published online by Cambridge University Press:
- 18 July 2013, pp. 671-700
- Print publication:
- October 2014
-
- Article
- Export citation
Generic pseudogroups on
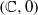 $( \mathbb{C} , 0)$ and the topology of leaves
$( \mathbb{C} , 0)$ and the topology of leaves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 8 / August 2013
- Published online by Cambridge University Press:
- 01 July 2013, pp. 1401-1430
- Print publication:
- August 2013
-
- Article
- Export citation
Rigid irregular connections on ℙ1
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 5 / September 2010
- Published online by Cambridge University Press:
- 22 April 2010, pp. 1323-1338
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
SHARP LOGARITHMIC DERIVATIVE ESTIMATES WITH APPLICATIONS TO ORDINARY DIFFERENTIAL EQUATIONS IN THE UNIT DISC
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 07 April 2010, pp. 145-167
- Print publication:
- April 2010
-
- Article
-
- You have access
- Export citation
Hypertranscendance des systèmes aux différences diagonaux
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 3 / May 2008
- Published online by Cambridge University Press:
- 01 May 2008, pp. 565-581
- Print publication:
- May 2008
-
- Article
-
- You have access
- Export citation
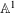
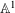
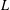
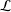
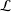
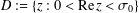
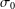
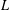
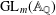
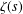
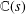

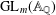
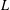
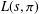
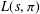
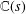
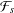
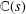
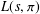
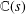
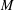
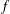
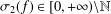

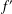
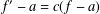

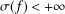
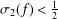
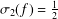
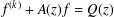

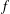
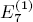 q-Painlevé system.
q-Painlevé system.