Refine listing
Actions for selected content:
28 results in 35Fxx
MICROLOCAL REGULARITY FOR MIZOHATA TYPE DIFFERENTIAL OPERATORS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 27 September 2018, pp. 1185-1209
- Print publication:
- July 2020
-
- Article
- Export citation
Solving the Equation
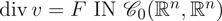 $\hbox{div}\, v = F\, \hbox{IN} {\cal C}_0(\open{R}^N, \open{R}^N)$
$\hbox{div}\, v = F\, \hbox{IN} {\cal C}_0(\open{R}^N, \open{R}^N)$
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 24 July 2018, pp. 1055-1061
-
- Article
- Export citation
Optimal stability estimates for continuity equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 6 / December 2018
- Published online by Cambridge University Press:
- 16 July 2018, pp. 1279-1296
- Print publication:
- December 2018
-
- Article
- Export citation
ON A CELL DIVISION EQUATION WITH A LINEAR GROWTH RATE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 59 / Issue 3 / January 2018
- Published online by Cambridge University Press:
- 26 February 2018, pp. 293-312
-
- Article
-
- You have access
- Export citation
Flows of measures generated by vector fields
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 4 / August 2018
- Published online by Cambridge University Press:
- 14 February 2018, pp. 773-818
- Print publication:
- August 2018
-
- Article
- Export citation
DEVELOPMENT OF A PROCESS MODEL FOR THE PREDICTION OF ABSORBENT DEGRADATION DURING
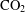 $\text{CO}_{2}$ CAPTURE
$\text{CO}_{2}$ CAPTURE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 16 August 2016, pp. 339-340
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
A convergence result for the ergodic problem for Hamilton–Jacobi equations with Neumann-type boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 03 March 2016, pp. 225-242
- Print publication:
- April 2016
-
- Article
- Export citation
On the local solvability of vector fields with critical points
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 10 / Issue 3 / July 2011
- Published online by Cambridge University Press:
- 12 May 2011, pp. 785-808
- Print publication:
- July 2011
-
- Article
- Export citation
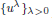 to a solution of the ergodic problem as λ → 0, and give a representation formula for the limit function via the Mather measures and Peierls function. As an interesting by-product, we introduce Mather measures associated with Hamilton–Jacobi equations with the Neumann-type boundary conditions. These results are variants of the main results in a recent paper by Davini
to a solution of the ergodic problem as λ → 0, and give a representation formula for the limit function via the Mather measures and Peierls function. As an interesting by-product, we introduce Mather measures associated with Hamilton–Jacobi equations with the Neumann-type boundary conditions. These results are variants of the main results in a recent paper by Davini 