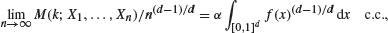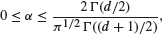Refine listing
Actions for selected content:
423 results in 60Dxx
Poisson limits for pairwise and area interaction point processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 75-85
- Print publication:
- March 2000
-
- Article
- Export citation
Compound Poisson approximation for the Johnson-Mehl model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 101-117
- Print publication:
- March 2000
-
- Article
- Export citation
Stationary countable dense random sets
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 86-100
- Print publication:
- March 2000
-
- Article
- Export citation
Existence of ‘nearest-neighbour’ spatial Gibbs models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 895-909
- Print publication:
- December 1999
-
- Article
- Export citation
Bounds for clump size characteristics in the Boolean model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 910-928
- Print publication:
- December 1999
-
- Article
- Export citation
Stochastic analysis of image acquisition, interpolation and scale-space smoothing
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 855-894
- Print publication:
- December 1999
-
- Article
- Export citation
Four interesting problems concerning Markovian shape sequences
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 954-968
- Print publication:
- December 1999
-
- Article
- Export citation
Surprising optimal estimators for the area fraction
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 995-1001
- Print publication:
- December 1999
-
- Article
- Export citation
The central limit theorem for Euclidean minimal spanning trees II
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 969-984
- Print publication:
- December 1999
-
- Article
- Export citation
The distribution of volume reductions induced by isotropic random projections
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 985-994
- Print publication:
- December 1999
-
- Article
- Export citation
On the size of a random sphere of influence graph
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 596-609
- Print publication:
- September 1999
-
- Article
- Export citation
Asymptotics for geometric location problems over random samples
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 632-642
- Print publication:
- September 1999
-
- Article
- Export citation
The volume fraction of a Poisson germ model with maximally non-overlapping spherical grains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 610-624
- Print publication:
- September 1999
-
- Article
- Export citation
Isotropic correlation functions on d-dimensional balls
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 625-631
- Print publication:
- September 1999
-
- Article
- Export citation
Interdependences of directional quantities of planar tessellations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 664-678
- Print publication:
- September 1999
-
- Article
- Export citation
Stopping sets: Gamma-type results and hitting properties
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 355-366
- Print publication:
- June 1999
-
- Article
- Export citation
Random p-content of a p-parallelotope in Euclidean n-space
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 343-354
- Print publication:
- June 1999
-
- Article
- Export citation
Central limit theorem for a class of random measures associated with germ-grain models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 283-314
- Print publication:
- June 1999
-
- Article
- Export citation
On connected component Markov point processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 279-282
- Print publication:
- June 1999
-
- Article
- Export citation
The convex hull of samples from self-similar distributions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 34-47
- Print publication:
- March 1999
-
- Article
- Export citation