Refine listing
Actions for selected content:
1705 results in 60Jxx
Extremes for shot noise processes with heavy tailed amplitudes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 643-656
- Print publication:
- September 1997
-
- Article
- Export citation
Detailed probabilistic analysis of the integrated three-valued telegraph signal
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 671-684
- Print publication:
- September 1997
-
- Article
- Export citation
Whole Genome Amplification and Branching Processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 629-668
- Print publication:
- September 1997
-
- Article
- Export citation
Limit theorems for the total size of a spatial epidemic
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 698-710
- Print publication:
- September 1997
-
- Article
- Export citation
Sooner waiting time problems in a sequence of trinary trials
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 593-609
- Print publication:
- September 1997
-
- Article
- Export citation
On the move-to-front scheme with Markov dependent requests
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 790-794
- Print publication:
- September 1997
-
- Article
- Export citation
Total Positivity of Markov Chains and the Failure Rate Character of Some First Passage Times
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 713-732
- Print publication:
- September 1997
-
- Article
- Export citation
The geometric convergence rate of a Lindley random walk
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 806-811
- Print publication:
- September 1997
-
- Article
- Export citation
Strong Approximations of Irreducible Closed Queueing Networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 498-522
- Print publication:
- June 1997
-
- Article
- Export citation
On the rate of convergence of Borovkov's multidimensional ergodic Markov chain
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 328-339
- Print publication:
- June 1997
-
- Article
- Export citation
A proof of the persistence criterion for a class of superprocesses
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 559-563
- Print publication:
- June 1997
-
- Article
- Export citation
A Bayesian analysis of layered defense systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 449-457
- Print publication:
- June 1997
-
- Article
- Export citation
The propagation of chaos of multitype mean field interacting particle systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 346-362
- Print publication:
- June 1997
-
- Article
- Export citation
Limit theorems and estimation theory for branching processes with an increasing random number of ancestors
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 309-327
- Print publication:
- June 1997
-
- Article
- Export citation
Sur Une Équation Fonctionnelle Et SES Applications: Une Extension Du Théorème De Kesten-Stigum Concernant Des Processus De Branchement
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 353-373
- Print publication:
- June 1997
-
- Article
- Export citation
A Geometric Product-Form Distribution for a Queueing Network by Non-Standard Batch Arrivals and Batch Transfers
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 523-544
- Print publication:
- June 1997
-
- Article
- Export citation
On the time a Markov chain spends in a lumped state
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 340-345
- Print publication:
- June 1997
-
- Article
- Export citation
Products of Irreducible Random Matrices in the (Max, +) Algebra
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 444-477
- Print publication:
- June 1997
-
- Article
- Export citation
On wald-type optimal stopping for Brownian motion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 1 / March 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 66-73
- Print publication:
- March 1997
-
- Article
- Export citation
The rate of occurrence of failures
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 1 / March 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 234-247
- Print publication:
- March 1997
-
- Article
- Export citation
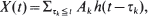 , where {
, where {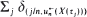 are shown to converge to a compound Poisson point process limit. As a corollary to this result, the joint limiting distribution of high local maxima is obtained.
are shown to converge to a compound Poisson point process limit. As a corollary to this result, the joint limiting distribution of high local maxima is obtained.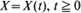 is examined. In particular, the third-order equations governing the distributions
is examined. In particular, the third-order equations governing the distributions 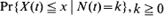 , (where
, (where 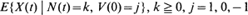 (where
(where 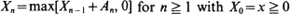 . Here, {
. Here, {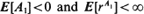 for some
for some 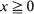 . In this communication we supply a short proof and some extensions of a large deviations result initially due to Veraverbeke and Teugels (1975, 1976): the largest
. In this communication we supply a short proof and some extensions of a large deviations result initially due to Veraverbeke and Teugels (1975, 1976): the largest  and
and 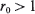 satisfies
satisfies 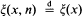 depends only on x. Sufficient conditions on moments of |
depends only on x. Sufficient conditions on moments of |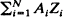 , where {Z
, where {Z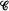 such that
such that 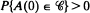 and the matrices
and the matrices 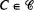 have a unique periodic regime.
have a unique periodic regime.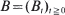 is standard Brownian motion and the supremum is taken over all stopping times
is standard Brownian motion and the supremum is taken over all stopping times 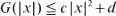 for some
for some 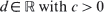 being given and fixed. The optimal stopping time is shown to be the hitting time by the reflecting Brownian motion
being given and fixed. The optimal stopping time is shown to be the hitting time by the reflecting Brownian motion 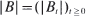 of the set of all (approximate) maximum points of the map
of the set of all (approximate) maximum points of the map 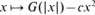 . The method of proof relies upon Wald's identity for Brownian motion and simple real analysis arguments. A simple proof of the Dubins–Jacka–Schwarz–Shepp–Shiryaev (square root of two) maximal inequality for randomly stopped Brownian motion is given as an application.
. The method of proof relies upon Wald's identity for Brownian motion and simple real analysis arguments. A simple proof of the Dubins–Jacka–Schwarz–Shepp–Shiryaev (square root of two) maximal inequality for randomly stopped Brownian motion is given as an application.