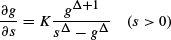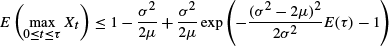Refine listing
Actions for selected content:
1705 results in 60Jxx
Optimal stopping and maximal inequalities for geometric Brownian motion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 4 / December 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 856-872
- Print publication:
- December 1998
-
- Article
- Export citation
The output process of an MMPP/M/1 queue
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 4 / December 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 998-1002
- Print publication:
- December 1998
-
- Article
- Export citation
Stability index for products of random transformations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 4 / December 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 968-988
- Print publication:
- December 1998
-
- Article
- Export citation
Estimation of the parameters of a branching process from migrating binomial observations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 4 / December 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 948-967
- Print publication:
- December 1998
-
- Article
- Export citation
Slow variation and uniqueness of solutions to the functional equation in the branching random walk
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 4 / December 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 795-801
- Print publication:
- December 1998
-
- Article
- Export citation
Hazard rate and reversed hazard rate monotonicities in continuous-time Markov chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 545-556
- Print publication:
- September 1998
-
- Article
- Export citation
A point process model with stochastic intensities for a branching population of two dependent types
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 723-739
- Print publication:
- September 1998
-
- Article
- Export citation
The Maclaurin series for performance functions of Markov chains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 676-692
- Print publication:
- September 1998
-
- Article
- Export citation
Immigration processes associated with branching particle systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 657-675
- Print publication:
- September 1998
-
- Article
- Export citation
A limit theorem for the maxima of the para-critical simple branching process
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 740-756
- Print publication:
- September 1998
-
- Article
- Export citation
Wald's equations, first passage times and moments of ladder variables in Markov random walks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 566-580
- Print publication:
- September 1998
-
- Article
- Export citation
Explicit sufficient invariants for an interacting particle system
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 633-641
- Print publication:
- September 1998
-
- Article
- Export citation
Applying POS(i) rules to communication problems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 762-769
- Print publication:
- September 1998
-
- Article
- Export citation
A threshold limit theorem for the stochastic logistic epidemic
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 662-670
- Print publication:
- September 1998
-
- Article
- Export citation
Some limit theorems for positive recurrent branching Markov chains: II
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 711-722
- Print publication:
- September 1998
-
- Article
- Export citation
A relatively quick way to simulate local random processes on a lattice
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 770-775
- Print publication:
- September 1998
-
- Article
- Export citation
Asymptotic probabilities in a sequential urn scheme related to the matchbox problem
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 831-849
- Print publication:
- September 1998
-
- Article
- Export citation
Some limit theorems for positive recurrent branching Markov chains: I
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 693-710
- Print publication:
- September 1998
-
- Article
- Export citation
The xlogx condition for general branching processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 537-544
- Print publication:
- September 1998
-
- Article
- Export citation
Truncation approximations of invariant measures for Markov chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 517-536
- Print publication:
- September 1998
-
- Article
- Export citation