Refine listing
Actions for selected content:
1705 results in 60Jxx
Exact and asymptotic solutions to a PDE that arises in time-dependent queues
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 256-283
- Print publication:
- March 2000
-
- Article
- Export citation
A new characterisation property of mixed Poisson processes via Berman's theorem
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 261-268
- Print publication:
- March 2000
-
- Article
- Export citation
An exponential change of measure for the Feller diffusion and some implications for superprocesses
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 236-245
- Print publication:
- March 2000
-
- Article
- Export citation
Geometric inequalities for the eigenvalues of concentrated Markov chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 15-28
- Print publication:
- March 2000
-
- Article
- Export citation
Compound Poisson approximation for the Johnson-Mehl model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 101-117
- Print publication:
- March 2000
-
- Article
- Export citation
Passage time moments for multidimensional diffusions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 246-251
- Print publication:
- March 2000
-
- Article
- Export citation
Asymptotic Behaviour of Continuous Time and State Branching Processes
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 1 / February 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 68-84
- Print publication:
- February 2000
-
- Article
-
- You have access
- Export citation
A note on acceptance rate criteria for CLTS for Metropolis–Hastings algorithms
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1210-1217
- Print publication:
- December 1999
-
- Article
- Export citation
Bounds for clump size characteristics in the Boolean model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 910-928
- Print publication:
- December 1999
-
- Article
- Export citation
Approximations of boundary crossing probabilities for a Brownian motion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1019-1030
- Print publication:
- December 1999
-
- Article
- Export citation
Generalized adaptive exponential smoothing of observations from an ergodic hidden Markov model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 987-998
- Print publication:
- December 1999
-
- Article
- Export citation
Duality results for block-structured transition matrices
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1045-1057
- Print publication:
- December 1999
-
- Article
- Export citation
A central limit theorem for super-Brownian motion with super-Brownian immigration
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1218-1224
- Print publication:
- December 1999
-
- Article
- Export citation
Four interesting problems concerning Markovian shape sequences
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 954-968
- Print publication:
- December 1999
-
- Article
- Export citation
Branching and tree indexed random walks on fractals
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 999-1011
- Print publication:
- December 1999
-
- Article
- Export citation
Bounded normal approximation in simulations of highly reliable Markovian systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 974-986
- Print publication:
- December 1999
-
- Article
- Export citation
Recent common ancestors of all present-day individuals
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1002-1026
- Print publication:
- December 1999
-
- Article
- Export citation
On the occurrence of composite events and clusters of points
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1012-1018
- Print publication:
- December 1999
-
- Article
- Export citation
Excursions of birth and death processes, orthogonal polynomials, and continued fractions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 752-770
- Print publication:
- September 1999
-
- Article
- Export citation
The distribution of time to extinction in subcritical branching processes: applications to outbreaks of infectious disease
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 771-779
- Print publication:
- September 1999
-
- Article
- Export citation
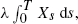 with λ > 0. The new processes can be thought of as ‘self-reinforcing’ versions of the old.
with λ > 0. The new processes can be thought of as ‘self-reinforcing’ versions of the old.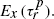 As an application we exhibit classes of diffusion processes which are recurrent but
As an application we exhibit classes of diffusion processes which are recurrent but 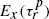 is infinite for all
is infinite for all 