Refine listing
Actions for selected content:
1705 results in 60Jxx
Level phase independence for GI/M/1-type Markov chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 4 / December 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 984-998
- Print publication:
- December 2000
-
- Article
- Export citation
On the lattice case of an almost-sure renewal theorem for branching random walks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 3 / September 2000
- Published online by Cambridge University Press:
- 19 February 2016, pp. 720-737
- Print publication:
- September 2000
-
- Article
- Export citation
Markov jump processes with a singularity
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 3 / September 2000
- Published online by Cambridge University Press:
- 19 February 2016, pp. 779-799
- Print publication:
- September 2000
-
- Article
- Export citation
Convergence to stationarity in the Moran model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 3 / September 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 705-717
- Print publication:
- September 2000
-
- Article
- Export citation
Joint distributions of successes, failures and patterns in enumeration problems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 3 / September 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 866-884
- Print publication:
- September 2000
-
- Article
- Export citation
The formal theory of birth-and-death processes, lattice path combinatorics and continued fractions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 3 / September 2000
- Published online by Cambridge University Press:
- 19 February 2016, pp. 750-778
- Print publication:
- September 2000
-
- Article
- Export citation
An unexpected connection between branching processes and optimal stopping
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 3 / September 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 613-626
- Print publication:
- September 2000
-
- Article
- Export citation
A stochastic lower bound for assemble-transfer batch service queueing networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 3 / September 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 881-889
- Print publication:
- September 2000
-
- Article
- Export citation
The time of completion of a linear birth-growth model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 3 / September 2000
- Published online by Cambridge University Press:
- 19 February 2016, pp. 620-627
- Print publication:
- September 2000
-
- Article
- Export citation
Explicit bounds for geometric convergence of Markov chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 3 / September 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 642-651
- Print publication:
- September 2000
-
- Article
- Export citation
A probabilistic proof of non-explosion of a non-linear PDE system
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 3 / September 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 635-641
- Print publication:
- September 2000
-
- Article
- Export citation
On the variance mean ratio in models of parasite distributions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 3 / September 2000
- Published online by Cambridge University Press:
- 19 February 2016, pp. 701-719
- Print publication:
- September 2000
-
- Article
- Export citation
Ornstein-Uhlenbeck type processes and branching processes with immigration
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 3 / September 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 627-634
- Print publication:
- September 2000
-
- Article
- Export citation
A note on the rate of convergence to equilibrium for Erlang's model in the subcritical case
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 3 / September 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 918-923
- Print publication:
- September 2000
-
- Article
- Export citation
Which design is better? Ehrenfest urn versus biased coin
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 3 / September 2000
- Published online by Cambridge University Press:
- 19 February 2016, pp. 738-749
- Print publication:
- September 2000
-
- Article
- Export citation
Families of birth-death processes with similar time-dependent behaviour
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 3 / September 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 835-849
- Print publication:
- September 2000
-
- Article
- Export citation
Filtering equations for the conditional law of residual lifetimes from a heterogeneous population
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 3 / September 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 823-834
- Print publication:
- September 2000
-
- Article
- Export citation
Continuous-time monotone stochastic recursions and duality
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 2 / June 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 426-445
- Print publication:
- June 2000
-
- Article
- Export citation
The Galton-Watson process revisited: some martingale relationships and applications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 2 / June 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 322-328
- Print publication:
- June 2000
-
- Article
- Export citation
Rates of convergence of stochastically monotone and continuous time Markov models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 2 / June 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 359-373
- Print publication:
- June 2000
-
- Article
- Export citation
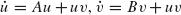 remain bounded for suitable bounded initial conditions, provided
remain bounded for suitable bounded initial conditions, provided 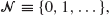 but allow the death rate in state 0 to be positive, so that escape from
but allow the death rate in state 0 to be positive, so that escape from 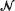 is possible. Two such processes with transition functions
is possible. Two such processes with transition functions 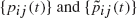 are said to be
are said to be 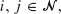 there are constants
there are constants 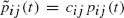 for all
for all 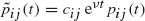 for all
for all 