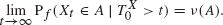Refine listing
Actions for selected content:
1705 results in 60Jxx
Optimal control of a dam using P λ,τ M policies and penalty cost when the input process is a compound Poisson process with positive drift
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 2 / June 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 408-416
- Print publication:
- June 2000
-
- Article
- Export citation
The correlated random walk with boundaries: A combinatorial solution
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 2 / June 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 470-479
- Print publication:
- June 2000
-
- Article
- Export citation
Domain of attraction of the quasi-stationary distributions for the Ornstein-Uhlenbeck process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 2 / June 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 511-520
- Print publication:
- June 2000
-
- Article
- Export citation
A note on uniformization for dynamic non-negative systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 2 / June 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 329-341
- Print publication:
- June 2000
-
- Article
- Export citation
Hypothesis testing and Skorokhod stochastic integration
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 2 / June 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 560-574
- Print publication:
- June 2000
-
- Article
- Export citation
Probabilistic models of DNA sequence evolution with context dependent rates of substitution
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 2 / June 2000
- Published online by Cambridge University Press:
- 19 February 2016, pp. 499-517
- Print publication:
- June 2000
-
- Article
- Export citation
Quasistationarity in continuous-time Markov chains where absorption is not certain
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 2 / June 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 598-600
- Print publication:
- June 2000
-
- Article
- Export citation
Explicit formulae for stationary distributions of stress release processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 2 / June 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 315-321
- Print publication:
- June 2000
-
- Article
- Export citation
On stability of nonlinear AR processes with Markov switching
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 2 / June 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 394-407
- Print publication:
- June 2000
-
- Article
- Export citation
The growth of general population-size-dependent branching processes year by year
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1-14
- Print publication:
- March 2000
-
- Article
- Export citation
The distributions of cluster functionals of extreme events in a dth-order Markov chain
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 29-44
- Print publication:
- March 2000
-
- Article
- Export citation
Markov paths on the Poisson-Delaunay graph with applications to routeing in mobile networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1-18
- Print publication:
- March 2000
-
- Article
- Export citation
Stochastic differential portfolio games
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 126-147
- Print publication:
- March 2000
-
- Article
- Export citation
Sensitivity analysis for Markov reward structures until entrance times
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 45-63
- Print publication:
- March 2000
-
- Article
- Export citation
Limit theorems for the minimal position in a branching random walk with independent logconcave displacements
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 159-176
- Print publication:
- March 2000
-
- Article
- Export citation
Jump-type Fleming-Viot processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 140-158
- Print publication:
- March 2000
-
- Article
- Export citation
Queueing networks with instantaneous movements: a unified approach by quasi-reversibility
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 284-313
- Print publication:
- March 2000
-
- Article
- Export citation
The ruin problem and cover times of asymmetric random walks and Brownian motions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 177-192
- Print publication:
- March 2000
-
- Article
- Export citation
A join the shorter queue model in heavy traffic
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 212-223
- Print publication:
- March 2000
-
- Article
- Export citation
Estimation of critical values in interacting particle systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 118-125
- Print publication:
- March 2000
-
- Article
- Export citation
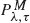 policies assuming that the input process is a compound Poisson process with a non-negative drift term, and using the total discounted cost and long-run average cost criteria. The results of Lee and Ahn (1998) as well as other well-known results are shown to follow from our results.
policies assuming that the input process is a compound Poisson process with a non-negative drift term, and using the total discounted cost and long-run average cost criteria. The results of Lee and Ahn (1998) as well as other well-known results are shown to follow from our results.