This paper is about the probability law of the integral of geometric Brownian motion over a finite time interval. A partial differential equation is derived for the Laplace transform of the law of the reciprocal integral, and is shown to yield an expression for the density of the distribution. This expression has some advantages over the ones obtained previously, at least when the normalized drift of the Brownian motion is a non-negative integer. Bougerol's identity and a relationship between Brownian motions with opposite drifts may also be seen to be special cases of these results.

Some consequences of restarting stochastic search algorithms are studied. It is shown under reasonable conditions that restarting when certain patterns occur yields probabilities that the goal state has not been found by the nth epoch which converge to zero at least geometrically fast in n. These conditions are shown to hold for restarted simulated annealing employing a local generation matrix, a cooling schedule T n ∼ c/n and restarting after a fixed number r + 1 of duplications of energy levels of states when r is sufficiently large. For simulated annealing with logarithmic cooling these probabilities cannot decrease to zero this fast. Numerical comparisons between restarted simulated annealing and several modern variations on simulated annealing are also presented and in all cases the former performs better.

We consider a repairable system with a finite state space which evolves in time according to a Markov process as long as it is working. We assume that this system is getting worse and worse while running: if the up-states are ranked according to their degree of increasing degradation, this is expressed by the fact that the Markov process is assumed to be monotone with respect to the reversed hazard rate and to have an upper triangular generator. We study this kind of process and apply the results to derive some properties of the stationary availability of the system. Namely, we show that, if the duration of the repair is independent of its completeness degree, then the more complete the repair, the higher the stationary availability, where the completeness degree of the repair is measured with the reversed hazard rate ordering.

Here we consider the Kohonen algorithm with a constant learning rate as a Markov process evolving in a topological space. Despite the fact that the algorithm is not weak Feller, we show that it is a T-chain, regardless of the dimensionalities of both data space and network and the special shape of the neighborhood function. In addition for the practically important case of the multi-dimensional setting, it is shown that the chain is irreducible and aperiodic. We show that these imply the validity of Doeblin's condition, which in turn ensures the convergence in distribution of the process to an invariant probability measure with a geometric rate. Furthermore, it is shown that the process is positive Harris recurrent, which enables us to use statistical devices to measure the centrality and variability of the invariant probability measure. Our results cover a wide class of neighborhood functions.

Wang and Pötzelberger (1997) derived an explicit formula for the probability that a Brownian motion crosses a one-sided piecewise linear boundary and used this formula to approximate the boundary crossing probability for general nonlinear boundaries. The present paper gives a sharper asymptotic upper bound of the approximation error for the formula, and generalizes the results to two-sided boundaries. Numerical computations are easily carried out using the Monte Carlo simulation method. A rule is proposed for choosing optimal nodes for the approximating piecewise linear boundaries, so that the corresponding approximation errors of boundary crossing probabilities converge to zero at a rate of O(1/n 2).

We consider a real-valued random walk which drifts to -∞ and is such that the step distribution is heavy tailed, say, subexponential. We investigate the asymptotic tail behaviour of the distribution of the upwards first passage times. As an application, we obtain the exact rate of convergence for the ruin probability in finite time. Our result supplements similar theorems in risk theory.

An explicit and computable criterion for strong ergodicity of single-birth processes is presented. As an application, some sufficient conditions are obtained for strong ergodicity of an extended class of continuous-time branching processes and multi-dimensional Q-processes by comparison methods respectively. Consequently strong ergodicity of the Q-process corresponding to the finite-dimensional Schlögl model is proven.

For a positive recurrent continuous-time Markov chain on a countable state space, we compare the access time to equilibrium to the hitting time of a particular state. For monotone processes, the exponential rates are ranked. When the process starts far from equilibrium, a cutoff phenomenon occurs at the same instant, in the sense that both the access time to equilibrium and the hitting time of a fixed state are equivalent to the expectation of the latter. In the case of Markov chains on trees, that expectation can be computed explicitly. The results are illustrated on the M/M/∞ queue.

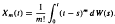Let {W(t), t ≥ 0} be a standard Brownian motion. For a positive integer m, define a Gaussian process Watanabe and Lachal gave some asymptotic properties of the process Xm(·), m ≥ 1. In this paper, we study the bounds of its moduli of continuity and large increments by establishing large deviation results.

Lenin et al. (2000) recently introduced the idea of similarity in the context of birth-death processes. This paper examines the extent to which their results can be extended to arbitrary Markov chains. It is proved that, under a variety of conditions, similar chains are strongly similar in a sense which is described, and it is shown that minimal chains are strongly similar if and only if the corresponding transition-rate matrices are strongly similar. A general framework is given for constructing families of strongly similar chains; it permits the construction of all such chains in the irreducible case.

The paper proves the statement of the title, and shows that it has useful applications in evaluating the convergence of queueing models and Gibbs samplers with deterministic and random scans.

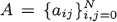The paper characterizes matrices which have a given system of vectors orthogonal with respect to a given probability distribution as its right eigenvectors. Results of Hoare and Rahman are unified in this context, then all matrices with a given orthogonal polynomial system as right eigenvectors under the constraint a 0j = 0 for j ≥ 2 are specified. The only stochastic matrices P = {pij } satisfying p 00 + p 01 = 1 with the Hahn polynomials as right eigenvectors have the form of the Moran mutation model.

The dynamics of host-macroparasite infections pose considerable challenges for stochastic modelling because of the need to take into account a large number of relevant factors and many nonlinear interactions between them. This paper focuses attention on the infection transmission process and the effects of specific modelling assumptions about the mechanisms involved. Some dramatically simplified linear models are considered; they are based on multidimensional linear birth and death processes, and are designed to illuminate qualitative effects of interest. Both single and compound infections are allowed. It is shown that such simple models can generate and increase dispersion of parasite counts, even among homogeneous hosts.

This paper considers the occurrence of patterns in sequences of independent trials from a finite alphabet; Gani and Irle (1999) have described a finite state automaton which identifies exactly those sequences of symbols containing the specific pattern, which may be thought of as the word of interest. Each word generates a particular Markov chain. Motivated by a result of Guibas and Odlyzko (1981) on stochastic monotonicity for the random times when a particular word is completed for the first time, a new level-crossing ordering is introduced for stochastic processes. A process {Yn : n = 0, 1, …} is slower in level-crossing than a process {Zn }, if it takes {Yn } stochastically longer than {Zn } to exceed any given level. This relation is shown to be useful for the comparison of stochastic automata, and is used to investigate this ordering for Markov chains in discrete time.

Haploid population models with non-overlapping generations and fixed population size N are considered. It is assumed that the family sizes ν1,…,νN within a generation are exchangeable random variables. Rates of convergence for the finite-dimensional distributions of a properly time-scaled ancestral coalescent process are established and expressed in terms of the transition probabilities of the ancestral process, i.e., in terms of the joint factorial moments of the offspring variables ν1,…,νN .

The Kingman coalescent appears in the limit as the population size N tends to infinity if and only if triple mergers are asymptotically negligible in comparison with binary mergers. In this case, a simple upper bound for the rate of convergence of the finite-dimensional distributions is derived. It depends (up to some constants) only on the three factorial moments E((ν1)2), E((ν1)3) and E((ν1)2(ν2)2), where (x)k := x(x-1)…(x-k+1). Examples are the Wright-Fisher model, where the rate of convergence is of order N -1, and the Moran model, with a convergence rate of order N -2.

Computer simulations had suggested that the strategy that maximises the score on each turn in the dice game described by Roters (1998) may not be the optimal way to reach a given target in the shortest time. We give an analytical treatment, backed by numerical calculations, that finds the optimal strategy to reach such a target.

For continuous-time Markov chains with semigroups P, P' taking values in a partially ordered set, such that P ≤ stP', we show the existence of an order-preserving Markovian coupling and give a way to construct it. From our proof, we also obtain the conditions of Brandt and Last for stochastic domination in terms of the associated intensity matrices. Our result is applied to get necessary and sufficient conditions for the existence of Markovian couplings between two Jackson networks.

A probabilistic proof of a Stein factor bound is given, extending the Poisson case in Xia (1999).

This paper introduces a fractional heat equation, where the diffusion operator is the composition of the Bessel and Riesz potentials. Sharp bounds are obtained for the variance of the spatial and temporal increments of the solution. These bounds establish the degree of singularity of the sample paths of the solution. In the case of unbounded spatial domain, a solution is formulated in terms of the Fourier transform of its spatially and temporally homogeneous Green function. The spectral density of the resulting solution is then obtained explicitly. The result implies that the solution of the fractional heat equation may possess spatial long-range dependence asymptotically.

We study a one-dimensional supercritical branching random walk in a non-i.i.d. random environment, which considers both the branching mechanism and the step transition. This random environment is constructed using a recurrent Markov chain on a finite or countable state space. Criteria of (strong) recurrence and transience are presented for this model.