Refine listing
Actions for selected content:
1705 results in 60Jxx
Outcomes of epidemic models with general infection and removal rate functions at certain stopping times
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 799-813
- Print publication:
- September 1999
-
- Article
- Export citation
On records and related processes for sequences with trends
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 668-681
- Print publication:
- September 1999
-
- Article
- Export citation
An iterative approximation scheme for repetitive Markov processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 654-667
- Print publication:
- September 1999
-
- Article
- Export citation
Characterizations, stochastic equations, and the Gibbs sampler
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 747-751
- Print publication:
- September 1999
-
- Article
- Export citation
A new stochastic model of microsatellite evolution
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 621-631
- Print publication:
- September 1999
-
- Article
- Export citation
Modelling hierarchical systems by a continuous-time homogeneous Markov chain using two-wave panel data
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 644-653
- Print publication:
- September 1999
-
- Article
- Export citation
Search schemes for random optimization algorithms that preserve the asymptotic distribution
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 825-836
- Print publication:
- September 1999
-
- Article
- Export citation
The fundamental matrix of singularly perturbed Markov chains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 679-697
- Print publication:
- September 1999
-
- Article
- Export citation
On the algebraic structure in Markovian processes of death and epidemic types
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 742-757
- Print publication:
- September 1999
-
- Article
- Export citation
On maximum family size in branching processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 632-643
- Print publication:
- September 1999
-
- Article
- Export citation
On some equalities of laws for Brownian motion with drift
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 682-687
- Print publication:
- September 1999
-
- Article
- Export citation
One-dimensional Kohonen maps are super-stable with exponential rate
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 367-393
- Print publication:
- June 1999
-
- Article
- Export citation
Elementary new proofs of classical limit theorems for Galton–Watson processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 301-309
- Print publication:
- June 1999
-
- Article
- Export citation
Asymptotic behaviour of population-size-dependent branching processes in Markovian random environments
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 611-619
- Print publication:
- June 1999
-
- Article
- Export citation
Reaching goals by a deadline: digital options and continuous-time active portfolio management
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 551-577
- Print publication:
- June 1999
-
- Article
- Export citation
Asymptotic behaviour for random walks in random environments
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 334-349
- Print publication:
- June 1999
-
- Article
- Export citation
On spectral gap estimates of a Markov chain via hitting times and coupling
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 310-319
- Print publication:
- June 1999
-
- Article
- Export citation
The Brownian excursion multi-dimensional local time density
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 350-373
- Print publication:
- June 1999
-
- Article
- Export citation
Optimal control of a truncated general immigration process through total catastrophes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 461-472
- Print publication:
- June 1999
-
- Article
- Export citation
Continuity for multi-type branching processes with varying environments
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 139-145
- Print publication:
- March 1999
-
- Article
- Export citation
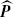 cannot be written as an exponential of an infinitesimal generator
cannot be written as an exponential of an infinitesimal generator 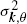 be the mean and the variance respectively of the offspring distribution when the population size is
be the mean and the variance respectively of the offspring distribution when the population size is 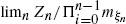 is studied in the case where sup
is studied in the case where sup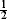 are small’, we show that there exists an invariant probability measure for ‘the environments seen from the position of (
are small’, we show that there exists an invariant probability measure for ‘the environments seen from the position of (