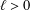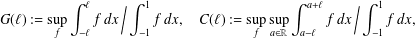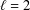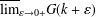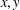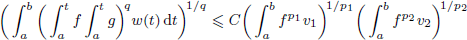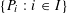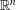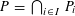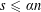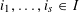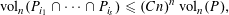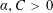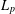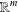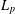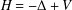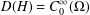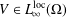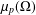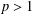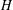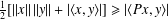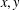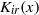Refine listing
Actions for selected content:
101 results in 26Dxx
Poincaré inequalities for Sobolev spaces with matrix-valued weights and applications to degenerate partial differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 22 April 2018, pp. 61-100
- Print publication:
- February 2019
-
- Article
- Export citation
Anisotropic Hardy inequalities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 20 December 2017, pp. 483-498
- Print publication:
- June 2018
-
- Article
- Export citation
A multi-species chemotaxis system: Lyapunov functionals, duality, critical mass
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 29 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 09 October 2017, pp. 515-542
-
- Article
- Export citation
SOME REVERSE DYNAMIC INEQUALITIES ON TIME SCALES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 17 August 2017, pp. 445-454
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
ON INTEGRAL ESTIMATES OF NONNEGATIVE POSITIVE DEFINITE FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 117-125
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
EXTENSIONS OF THE HERMITE–HADAMARD INEQUALITY FOR
 $r$ -PREINVEX FUNCTIONS ON AN INVEX SET
$r$ -PREINVEX FUNCTIONS ON AN INVEX SET
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 06 March 2017, pp. 412-423
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
NEW ALGEBRAIC-TRIGONOMETRIC INEQUALITIES OF LAUB–ILANI TYPE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 02 March 2017, pp. 87-97
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
Iterating Bilinear Hardy Inequalities
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 30 January 2017, pp. 955-971
-
- Article
- Export citation
BRASCAMP–LIEB INEQUALITY AND QUANTITATIVE VERSIONS OF HELLY’S THEOREM
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 07 December 2016, pp. 272-291
- Print publication:
- 2017
-
- Article
- Export citation
ON THE VARIATIONAL CONSTANT ASSOCIATED TO THE
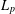 $L_{p}$ -HARDY INEQUALITY
$L_{p}$ -HARDY INEQUALITY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 23 September 2016, pp. 405-419
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
Optimal rearrangement invariant range for Hardy-type operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 4 / August 2016
- Published online by Cambridge University Press:
- 12 May 2016, pp. 865-893
- Print publication:
- August 2016
-
- Article
- Export citation
BUZANO’S INEQUALITY HOLDS FOR ANY PROJECTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 20 January 2016, pp. 504-510
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
EXACT UPPER AND LOWER BOUNDS ON THE DIFFERENCE BETWEEN THE ARITHMETIC AND GEOMETRIC MEANS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 04 May 2015, pp. 149-158
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
CONCAVITY PROPERTIES OF EXTENSIONS OF THE PARALLEL VOLUME
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 13 January 2015, pp. 266-282
- Print publication:
- 2016
-
- Article
- Export citation
FRACTIONAL SOBOLEV–POINCARÉ AND FRACTIONAL HARDY INEQUALITIES IN UNBOUNDED JOHN DOMAINS
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 20 October 2014, pp. 385-401
- Print publication:
- May 2015
-
- Article
- Export citation
SHARP CONSTANTS IN THE POINCARÉ, STEKLOV AND RELATED INEQUALITIES (A SURVEY)
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 10 October 2014, pp. 328-344
- Print publication:
- May 2015
-
- Article
- Export citation
THE REFLEXIVITY INDEX OF A LATTICE OF SETS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 25 July 2014, pp. 237-250
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
SOME INEQUALITIES OF JENSEN TYPE FOR ARG-SQUARE CONVEX FUNCTIONS OF UNITARY OPERATORS IN HILBERT SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 12 May 2014, pp. 65-73
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
SOME RESULTS ON COMPARING TWO INTEGRAL MEANS FOR ABSOLUTELY CONTINUOUS FUNCTIONS AND APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 10 April 2014, pp. 264-274
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
Bounds and algorithms for the
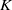 $K$ -Bessel function of imaginary order
$K$ -Bessel function of imaginary order
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 10 April 2013, pp. 78-108
-
- Article
-
- You have access
- Export citation