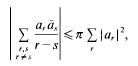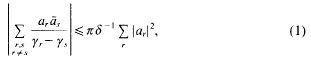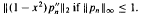Refine listing
Actions for selected content:
101 results in 26Dxx
ANOTHER SHARP L2 INEQUALITY OF OSTROWSKI TYPE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 1 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 129-136
-
- Article
-
- You have access
- Export citation
ARITHMETIC MEAN OF VALUES AND VALUE AT MEAN OF ARGUMENTS FOR CONVEX FUNCTIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 1 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 137-141
-
- Article
-
- You have access
- Export citation
INEQUALITIES FOR SUPERADDITIVE FUNCTIONALS WITH APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 401-411
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
A NEW MEAN WITH INEQUALITIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 365-371
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
MULTIDIMENSIONAL HARDY-TYPE INEQUALITIES VIA CONVEXITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 245-260
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
APPROXIMATING THE STIELTJES INTEGRAL FOR (φ,Φ)-LIPSCHITZIAN INTEGRATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 73-90
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation
A SHARP L2 INEQUALITY OF OSTROWSKI TYPE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 3 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 423-429
-
- Article
-
- You have access
- Export citation
Some completely monotonic functions involving the gamma and polygamma functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 1 / February 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 81-88
- Print publication:
- February 2006
-
- Article
-
- You have access
- Export citation
A further generalization of Hilbert's inequality
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 35-39
- Print publication:
- June 1999
-
- Article
- Export citation
Still more generalizations of Hardy's inequality
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 2 / October 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 214-224
- Print publication:
- October 1995
-
- Article
-
- You have access
- Export citation
Markoff type inequalities for curved majorants
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 1 / February 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-14
- Print publication:
- February 1995
-
- Article
-
- You have access
- Export citation
Opial-type inequalities with m functions in n variables
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 319-326
- Print publication:
- December 1992
-
- Article
- Export citation
Certain inequalities involving fractional powers
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 53 / Issue 1 / August 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 131-136
- Print publication:
- August 1992
-
- Article
-
- You have access
- Export citation
Some inequalities of Bessel and modified Bessel functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 2 / April 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 333-342
- Print publication:
- April 1991
-
- Article
-
- You have access
- Export citation
On some reverse integral inequalities
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 2 / October 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 319-326
- Print publication:
- October 1990
-
- Article
-
- You have access
- Export citation
Some new Opial-type inequalities
- Part of
-
- Journal:
- Mathematika / Volume 37 / Issue 1 / June 1990
- Published online by Cambridge University Press:
- 26 February 2010, pp. 136-142
- Print publication:
- June 1990
-
- Article
- Export citation
Integral inequalities resembling Copson's inequality
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 48 / Issue 1 / February 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 124-132
- Print publication:
- February 1990
-
- Article
-
- You have access
- Export citation
Some inequalities that arise in measure theory
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 45 / Issue 1 / August 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 83-94
- Print publication:
- August 1988
-
- Article
-
- You have access
- Export citation
On the convexity and symmetry of solutions to an elliptic free boundary problem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 42 / Issue 1 / February 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 57-68
- Print publication:
- February 1987
-
- Article
-
- You have access
- Export citation
Some inequalities for trigonometric polynomials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 2 / October 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 216-226
- Print publication:
- October 1985
-
- Article
-
- You have access
- Export citation
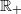 for some positive constants
for some positive constants 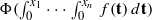 instead of
instead of 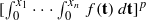 , while the corresponding right-hand sides remain as in the classical Hardy’s inequality and have explicit constants in front of integrals. We also prove the related dual inequalities. The relations obtained are new even for the one-dimensional case and they unify and extend several inequalities of Hardy type known in the literature.
, while the corresponding right-hand sides remain as in the classical Hardy’s inequality and have explicit constants in front of integrals. We also prove the related dual inequalities. The relations obtained are new even for the one-dimensional case and they unify and extend several inequalities of Hardy type known in the literature.