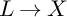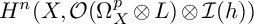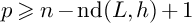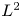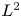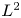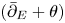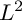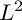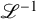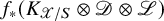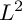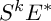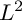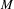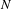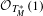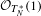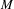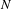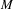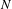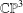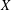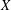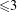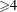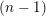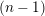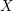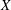Refine listing
Actions for selected content:
26 results in 32Lxx
Aspherical complex surfaces, the Singer conjecture, and Gromov–Lück inequality
 $\chi \ge |\sigma |$
$\chi \ge |\sigma |$
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 3 / November 2025
- Published online by Cambridge University Press:
- 17 July 2025, pp. 541-555
- Print publication:
- November 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COHERENCE OF MULTIPLIER SUBMODULE SHEAVES ON GENERIC COMPLEX TORI
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 30 June 2025, pp. 1-8
-
- Article
- Export citation
Invariant divisors and equivariant line bundles
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 03 April 2025, e68
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXTENSION OF COHOMOLOGY CLASSES FOR VECTOR BUNDLES WITH SINGULAR HERMITIAN METRICS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 259 / September 2025
- Published online by Cambridge University Press:
- 17 February 2025, pp. 562-580
- Print publication:
- September 2025
-
- Article
- Export citation
ON A BOGOMOLOV TYPE VANISHING THEOREM
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 257 / March 2025
- Published online by Cambridge University Press:
- 13 January 2025, pp. 170-182
- Print publication:
- March 2025
-
- Article
- Export citation
Vanishing theorem for tame harmonic bundles via L2-cohomology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 03 April 2025, pp. 2828-2855
- Print publication:
- December 2024
-
- Article
- Export citation
DUAL NAKANO POSITIVITY AND SINGULAR NAKANO POSITIVITY OF DIRECT IMAGE SHEAVES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 257 / March 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 55-78
- Print publication:
- March 2025
-
- Article
- Export citation
Singer conjecture for varieties with semismall Albanese map and residually finite fundamental group
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 19 April 2024, pp. 1-7
-
- Article
- Export citation
Positivity of Schur forms for strongly decomposably positive vector bundles
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 08 January 2024, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONCAVITY PROPERTY OF MINIMAL
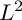 $L^{2}$ INTEGRALS WITH LEBESGUE MEASURABLE GAIN
$L^{2}$ INTEGRALS WITH LEBESGUE MEASURABLE GAIN
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 252 / December 2023
- Published online by Cambridge University Press:
- 05 June 2023, pp. 842-905
- Print publication:
- December 2023
-
- Article
- Export citation
Positivity of direct images with a Poincaré type twist
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 18 October 2022, e89
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SINGULAR HERMITIAN METRICS WITH ISOLATED SINGULARITIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 10 June 2022, pp. 980-989
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
POSITIVELY CURVED FINSLER METRICS ON VECTOR BUNDLES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 08 March 2022, pp. 766-778
- Print publication:
- December 2022
-
- Article
- Export citation
RC-positive metrics on rationally connected manifolds
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 16 November 2020, e53
-
- Article
-
- You have access
- Open access
- Export citation
Orbifold hyperbolicity
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 08 October 2020, pp. 1664-1698
- Print publication:
- August 2020
-
- Article
- Export citation
RC-POSITIVITY, VANISHING THEOREMS AND RIGIDITY OF HOLOMORPHIC MAPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 11 October 2019, pp. 1023-1038
- Print publication:
- May 2021
-
- Article
- Export citation
ALGEBRAIC SURFACES WITH INFINITELY MANY TWISTOR LINES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 24 May 2019, pp. 61-70
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
OBSTRUCTIONS TO ALGEBRAIZING TOPOLOGICAL VECTOR BUNDLES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 21 March 2019, e6
-
- Article
-
- You have access
- Open access
- Export citation
A partial converse to the Andreotti–Grauert theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 19 November 2018, pp. 89-99
- Print publication:
- January 2019
-
- Article
- Export citation
Numerical dimension and a Kawamata–Viehweg–Nadel-type vanishing theorem on compact Kähler manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 11 / November 2014
- Published online by Cambridge University Press:
- 27 August 2014, pp. 1869-1902
- Print publication:
- November 2014
-
- Article
- Export citation