This article investigates the accuracy of approximations for the distribution of ordered m-spacings for i.i.d. uniform observations in the interval (0, 1). Several Poisson approximations and a compound Poisson approximation are studied. The result of a simulation study is included to assess the accuracy of these approximations. A numerical procedure for evaluating the moments of the ordered m-spacings is developed and evaluated for the most accurate approximation.

A family of distribution-free statistics along with related tests is defined and properties of its members are studied. These statistics, one of which is the Smirnov-Wald and Wolfowitz statistic, D n + yield tests of the one-sided hypotheses. The minimax and maximin tests in this family against a restricted class of alternatives of minimum power are obtained. The connection to a confidence bound of Stringer for the mean is also remarked.

The accuracy of the Poisson approximation to the distribution of the numbers of large and small m-spacings, when n points are placed at random on the circle, was analysed using the Stein–Chen method in Barbour et al. (1992b). The Poisson approximation for m≧2 was found not to be as good as for 1-spacings. In this paper, rates of approximation of these distributions to suitable compound Poisson distributions are worked out, using the CP–Stein–Chen method and an appropriate coupling argument. The rates are better than for Poisson approximation for m≧2, and are of order O((log n)2/n) for large m-spacings and of order O(1/n) for small m-spacings, for any fixed m≧2, if the expected number of spacings is held constant as n → ∞.

Limits in distribution of maxima of independent stochastic processes are characterized in terms of spectral functions acting on a Poisson point process.

Let Qn denote the number of times where a simple random walk reaches its maximum, where the random walk starts at the origin and returns to the origin after 2n steps. Such random walks play an important role in probability and statistics. In this paper the distribution and the moments of Qn , are considered and their asymptotic behavior is studied.

Estimators which have locally uniform expansions are shown in this paper to be asymptotically equivalent to M-estimators. The M-functionals corresponding to these M-estimators are seen to be locally uniformly Fréchet differentiable. Other conditions for M-functionals to be locally uniformly Fréchet differentiable are given. An example of a commonly used estimator which is robust against outliers is given to illustrate that the locally uniform expansion need not be valid.

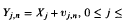Consider the additive effects outliers (A.O.) model where one observes , with 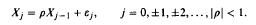The sequence of r.v.s 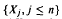is independent of 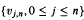and 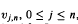, are i.i.d. with d.f. 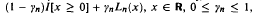, where the d.f.s Ln, n ≦ 0, are not necessarily known and εj's are i.i.d.. This paper discusses the asymptotic behavior of functional least squares estimators under the above model. Uniform consistency and uniform strong consistency of these estimators are proven. The weak convergence of these estimators to a Gaussian process and their asymptotic biases are also discussed under the above A.O. model.

We show that stochastic compactness of partial sums with no normal limit distribution corresponds to stochastic compactness of the point processes generated by the observations so that there exist joint limit distributions for the sample sums and the sample maxima.