Logarithmic asymptotics of the mean process {S n ∕n} are investigated in the presence of heavy-tailed increments. As a consequence, a full large deviations principle for means is obtained when the hazard function of an increment is regularly varying with index α∈(0,1). This class includes all stretched exponential distributions. Thus, the previous research of Gantert et al. (2014) is extended. Furthermore, the presented proofs are more transparent than the techniques used by Nagaev (1979). In addition, the novel approach is compatible with other common classes of distributions, e.g. those of lognormal type.

The subject of this paper is the problem of estimating the service time distribution of the M/G/∞ queue from incomplete data on the queue. The goal is to estimate G from observations of the queue-length process at the points of the regular grid on a fixed time interval. We propose an estimator and analyze its accuracy over a family of target service time distributions. An upper bound on the maximal risk is derived. The problem of estimating the arrival rate is considered as well.

An extended model of order statistics based on possibly different distributions is introduced and analyzed. In the interpretation of successive failure times in a 𝑘-out-of-𝑛 system, say, until each failure, the time periods under previous (increasing) loads exerted on the remaining components are recorded. Then the lifetime distribution of the system depends on the complete failure scheme. Thus, order statistics with memory provide an alternative to the use of sequential order statistics, which form a Markov chain. The quantities as well as their spacings, the interoccurrence times, can be compared by means of stochastic ordering.

In this paper we give a simple proof of a limit theorem for the length of the largest interval straddling a fixed number of points that are independent and uniformly distributed on a unit interval. The key step in our argument is a classical theorem of Watson on the maxima of m-dependent stationary stochastic sequences.

We perform an analysis of the potential time inhomogeneity in the dependence between multiple financial time series. To this end, we use the framework of copula theory and tackle the question of whether dependencies in such a case can be assumed constant throughout time or rather have to be modeled in a time-inhomogeneous way. We focus on parametric copula models and suitable inference techniques in the context of a special copula-based multivariate time series model. A recent result due to Chan et al. (2009) is used to derive the joint limiting distribution of local maximum-likelihood estimators on overlapping samples. By restricting the overlap to be fixed, we establish the limiting law of the maximum of the estimator series. Based on the limiting distributions, we develop statistical homogeneity tests, and investigate their local power properties. A Monte Carlo simulation study demonstrates that bootstrapped variance estimates are needed in finite samples. Empirical analyses on real-world financial data finally confirm that time-varying parameters are an exception rather than the rule.

A Poisson line tessellation is observed in the window Wρ := B(0, π-1/2ρ1/2) for ρ > 0. With each cell of the tessellation, we associate the inradius, which is the radius of the largest ball contained in the cell. Using the Poisson approximation, we compute the limit distributions of the largest and smallest order statistics for the inradii of all cells whose nuclei are contained in Wρ as ρ goes to ∞. We additionally prove that the limit shape of the cells minimising the inradius is a triangle.

In this paper we consider a classic problem concerning the high excursion probabilities of a Gaussian random field f living on a compact set T. We develop efficient computational methods for the tail probabilities ℙ{supT f(t) > b}. For each positive ε, we present Monte Carlo algorithms that run in constant time and compute the probabilities with relative error ε for arbitrarily large b. The efficiency results are applicable to a large class of Hölder continuous Gaussian random fields. Besides computations, the change of measure and its analysis techniques have several theoretical and practical indications in the asymptotic analysis of Gaussian random fields.

Let X λ1 , X λ2 , …, X λ n be independent Weibull random variables with X λ i ∼ W(α, λi ), where λi > 0 for i = 1, …, n. Let X n:n λ denote the lifetime of the parallel system formed from X λ1 , X λ2 , …, X λ n . We investigate the effect of the changes in the scale parameters (λ1, …, λn ) on the magnitude of X n:n λ according to reverse hazard rate and likelihood ratio orderings.

We consider semicoherent and mixed systems with exchangeable components. We present sharp lower and upper bounds on various dispersion measures (in particular, variance and median absolute deviation) of the system lifetime, expressed in terms of the system signature and the dispersion of a single component lifetime. We construct joint exchangeable distributions of component lifetimes with two-point marginals which attain the bounds in the limit.

In this paper we consider the stationary Poisson Boolean model with spherical grains and propose a family of nonparametric estimators for the radius distribution. These estimators are based on observed distances and radii, weighted in an appropriate way. They are ratio unbiased and asymptotically consistent for a growing observation window. We show that the asymptotic variance exists and is given by a fairly explicit integral expression. Asymptotic normality is established under a suitable integrability assumption on the weight function. We also provide a short discussion of related estimators as well as a simulation study.

In this paper we provide the basis for new methods of inference for max-stable processes ξ on general spaces that admit a certain incremental representation, which, in important cases, has a much simpler structure than the max-stable process itself. A corresponding peaks-over-threshold approach will incorporate all single events that are extreme in some sense and will therefore rely on a substantially larger amount of data in comparison to estimation procedures based on block maxima. Conditioning a process η in the max-domain of attraction of ξ on being extremal, several convergence results for the increments of η are proved. In a similar way, the shape functions of mixed moving maxima (M3) processes can be extracted from suitably conditioned single events η. Connecting the two approaches, transformation formulae for processes that admit both an incremental and an M3 representation are identified.

The generalized Pólya urn has been extensively studied and is widely applied in many disciplines. An important application of urn models is in the development of randomized treatment allocation schemes in clinical studies. The randomly reinforced urn was recently proposed, but, although the model has some intuitively desirable properties, it lacks theoretical justification. In this paper we obtain important asymptotic properties for multicolor reinforced urn models. We derive results for the rate of convergence of the number of patients assigned to each treatment under a set of minimum required conditions and provide the distributions of the limits. Furthermore, we study the asymptotic behavior for the nonhomogeneous case.

The idea of the system signature is extended here to the case of ordered system lifetimes arising from a test of coherent systems with a signature. An expression is given for the computation of the ordered system signatures in terms of the usual system signature for system lifetimes. Some properties of the ordered system signatures are then established. Closed-form expressions for the ordered system signatures are obtained in some special cases, and some illustrative examples are presented.

In this paper we study nonparametric estimation problems for a class of piecewise-deterministic Markov processes (PDMPs). Borovkov and Last (2008) proved a version of Rice's formula for PDMPs, which explains the relation between the stationary density and the level crossing intensity. From a statistical point of view, their result suggests a methodology for estimating the stationary density from observations of a sample path of PDMPs. First, we introduce the local time related to the level crossings and construct the local-time estimator for the stationary density, which is unbiased and uniformly consistent. Secondly, we investigate other estimation problems for the jump intensity and the conditional jump size distribution.

Wicksell's classical corpuscle problem deals with the retrieval of the size distribution of spherical particles from planar sections. We discuss the problem in a local stereology framework. Each particle is assumed to contain a reference point and the individual particle is sampled with an isotropic random plane through this reference point. Both the size of the section profile and the position of the reference point inside the profile are recorded and used to recover the distribution of the corresponding particle parameters. Theoretical results concerning the relationship between the profile and particle parameters are discussed. We also discuss the unfolding of the arising integral equations, uniqueness issues, and the domain of attraction relations. We illustrate the approach by providing reconstructions from simulated data using numerical unfolding algorithms.

Multivariate regular variation plays a role in assessing tail risk in diverse applications such as finance, telecommunications, insurance, and environmental science. The classical theory, being based on an asymptotic model, sometimes leads to inaccurate and useless estimates of probabilities of joint tail regions. This problem can be partly ameliorated by using hidden regular variation (see Resnick (2002) and Mitra and Resnick (2011)). We offer a more flexible definition of hidden regular variation that provides improved risk estimates for a larger class of tail risk regions.

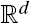Let M be a bounded domain of with a smooth boundary. We relate the Cheeger constant of M and the conductance of a neighborhood graph defined on a random sample from M. By restricting the minimization defining the latter over a particular class of subsets, we obtain consistency (after normalization) as the sample size increases, and show that any minimizing sequence of subsets has a subsequence converging to a Cheeger set of M.