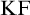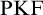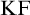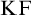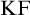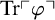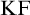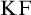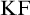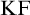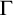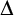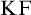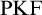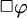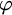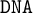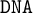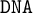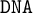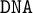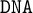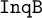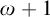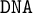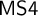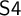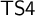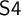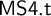Refine search
Actions for selected content:
4250 results in Numerical analysis and computational science
7 - Multivariate Quasi-Interpolants: Construction in n Dimensions
-
- Book:
- Quasi-Interpolation
- Published online:
- 24 February 2022
- Print publication:
- 03 March 2022, pp 143-170
-
- Chapter
- Export citation
RSL volume 15 issue 1 Cover and Back matter
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 16 March 2022, pp. b1-b2
- Print publication:
- March 2022
-
- Article
-
- You have access
- Export citation
RSL volume 15 issue 1 Cover and Front matter
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 16 March 2022, pp. f1-f4
- Print publication:
- March 2022
-
- Article
-
- You have access
- Export citation

Quasi-Interpolation
-
- Published online:
- 24 February 2022
- Print publication:
- 03 March 2022
A SIMPLE SEQUENT SYSTEM FOR MINIMALLY INCONSISTENT LP
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 23 February 2022, pp. 1296-1311
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RIGOUR AND PROOF – CORRIGENDUM
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 22 February 2022, p. 338
- Print publication:
- March 2023
-
- Article
-
- You have access
- HTML
- Export citation
TOWARDS THE INEVITABILITY OF NON-CLASSICAL PROBABILITY
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 21 February 2022, pp. 1053-1079
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
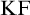 $\mathrm {KF}$,
$\mathrm {KF}$, 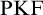 $\mathrm {PKF}$, AND REINHARDT’S PROGRAM
$\mathrm {PKF}$, AND REINHARDT’S PROGRAM
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 08 February 2022, pp. 33-58
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PLURAL ANCESTRAL LOGIC AS THE LOGIC OF ARITHMETIC
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 07 February 2022, pp. 305-342
- Print publication:
- June 2024
-
- Article
- Export citation
MEREOLOGICAL BIMODAL LOGICS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 27 January 2022, pp. 823-858
- Print publication:
- December 2022
-
- Article
- Export citation
A SUBSTRUCTURAL GENTZEN CALCULUS FOR ORTHOMODULAR QUANTUM LOGIC
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 27 January 2022, pp. 1177-1198
- Print publication:
- December 2023
-
- Article
- Export citation
RAMSIFICATION AND SEMANTIC INDETERMINACY
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 04 January 2022, pp. 900-950
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MODES OF CONVERGENCE TO THE TRUTH: STEPS TOWARD A BETTER EPISTEMOLOGY OF INDUCTION
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 03 January 2022, pp. 277-310
- Print publication:
- June 2022
-
- Article
- Export citation
THE GENEALOGY OF ‘
 $\mathbin {\boldsymbol {\vee }}$’
$\mathbin {\boldsymbol {\vee }}$’
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 03 January 2022, pp. 862-899
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stit-LOGIC FOR IMAGINATION EPISODES WITH VOLUNTARY INPUT
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 06 December 2021, pp. 813-861
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SZEMERÉDI’S THEOREM: AN EXPLORATION OF IMPURITY, EXPLANATION, AND CONTENT
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 03 December 2021, pp. 700-739
- Print publication:
- September 2023
-
- Article
- Export citation
LEIBNIZ ON BODIES AND INFINITIES: RERUM NATURA AND MATHEMATICAL FICTIONS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 03 December 2021, pp. 36-66
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN ALGEBRAIC APPROACH TO INQUISITIVE AND
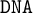 $\mathtt {DNA}$-LOGICS
$\mathtt {DNA}$-LOGICS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 02 December 2021, pp. 950-990
- Print publication:
- December 2022
-
- Article
- Export citation
GÖDEL’S THEOREM AND DIRECT SELF-REFERENCE
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 02 December 2021, pp. 650-654
- Print publication:
- June 2023
-
- Article
- Export citation
TEMPORAL INTERPRETATION OF MONADIC INTUITIONISTIC QUANTIFIERS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 02 December 2021, pp. 164-187
- Print publication:
- March 2023
-
- Article
- Export citation