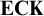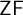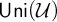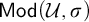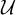Refine search
Actions for selected content:
4250 results in Numerical analysis and computational science
Deep learning: a statistical viewpoint
-
- Journal:
- Acta Numerica / Volume 30 / May 2021
- Published online by Cambridge University Press:
- 04 August 2021, pp. 87-201
-
- Article
-
- You have access
- Open access
- Export citation
Neural network approximation
-
- Journal:
- Acta Numerica / Volume 30 / May 2021
- Published online by Cambridge University Press:
- 04 August 2021, pp. 327-444
-
- Article
-
- You have access
- Open access
- Export citation
ANU volume 30 Cover and Back matter
-
- Journal:
- Acta Numerica / Volume 30 / May 2021
- Published online by Cambridge University Press:
- 04 August 2021, p. b1
-
- Article
-
- You have access
- Export citation
ANU volume 30 Cover and Front matter
-
- Journal:
- Acta Numerica / Volume 30 / May 2021
- Published online by Cambridge University Press:
- 04 August 2021, pp. f1-f6
-
- Article
-
- You have access
- Export citation
Numerical homogenization beyond scale separation
-
- Journal:
- Acta Numerica / Volume 30 / May 2021
- Published online by Cambridge University Press:
- 04 August 2021, pp. 1-86
-
- Article
-
- You have access
- Open access
- Export citation
CONDITIONAL LOGIC IS COMPLETE FOR CONVEXITY IN THE PLANE
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 08 July 2021, pp. 529-552
- Print publication:
- June 2023
-
- Article
- Export citation
THREE MODEL-THEORETIC CONSTRUCTIONS FOR GENERALIZED EPSTEIN SEMANTICS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 08 July 2021, pp. 1023-1032
- Print publication:
- December 2022
-
- Article
- Export citation
HIERARCHICAL INCOMPLETENESS RESULTS FOR ARITHMETICALLY DEFINABLE EXTENSIONS OF FRAGMENTS OF ARITHMETIC
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 14 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 02 July 2021, pp. 624-644
- Print publication:
- September 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NEIGHBOURHOOD CANONICITY FOR EK, ECK, AND RELATIVES: A CONSTRUCTIVE PROOF
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 02 July 2021, pp. 607-623
- Print publication:
- September 2022
-
- Article
- Export citation
A CORRECTNESS PROOF FOR AL-BARAKĀT’S LOGICAL DIAGRAMS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 02 July 2021, pp. 369-384
- Print publication:
- June 2023
-
- Article
- Export citation
IMPROVING STRONG NEGATION
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 02 July 2021, pp. 951-977
- Print publication:
- September 2023
-
- Article
- Export citation
A MATHEMATICAL COMMITMENT WITHOUT COMPUTATIONAL STRENGTH
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 02 July 2021, pp. 880-906
- Print publication:
- December 2022
-
- Article
- Export citation
RUSSELLIAN DEFINITE DESCRIPTION THEORY—A PROOF THEORETIC APPROACH
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 02 July 2021, pp. 624-649
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SUBATOMIC INFERENCES: AN INFERENTIALIST SEMANTICS FOR ATOMICS, PREDICATES, AND NAMES
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 02 July 2021, pp. 672-699
- Print publication:
- September 2023
-
- Article
- Export citation
INTERPRETATION, LOGIC AND PHILOSOPHY: JEAN NICOD’S GEOMETRY IN THE SENSIBLE WORLD
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 02 July 2021, pp. 1080-1109
- Print publication:
- December 2023
-
- Article
- Export citation
LOGICS OF FORMAL INCONSISTENCY ENRICHED WITH REPLACEMENT: AN ALGEBRAIC AND MODAL ACCOUNT
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 02 July 2021, pp. 771-806
- Print publication:
- September 2022
-
- Article
- Export citation
THE COPERNICAN MULTIVERSE OF SETS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 14 June 2021, pp. 1033-1069
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RSL volume 14 issue 2 Cover and Back matter
-
- Journal:
- The Review of Symbolic Logic / Volume 14 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 15 July 2021, pp. b1-b2
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
RSL volume 14 issue 2 Cover and Front matter
-
- Journal:
- The Review of Symbolic Logic / Volume 14 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 15 July 2021, pp. f1-f4
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
QUANTIFIED MODAL RELEVANT LOGICS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 23 April 2021, pp. 210-240
- Print publication:
- March 2023
-
- Article
- Export citation